题目内容
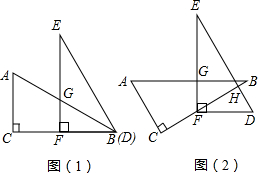
9.已知两个大小相同的含30°角的直角三角板ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G.直线BC与DE交于点H,∠C=∠EFB=90°,∠E=∠ABC=30°.(1)如图(2)将三角板ABC绕点F逆时针旋转一个大小为α的角,当AB∥FD时,求∠EGB+α的度数;
(2)在将三角板ABC绕点F逆时针旋转α角(0°<α<60°)的过程中,请你判断∠EGB与α的数量关系是否发生变化;如果不变,请写出并证明这个关系;如果改变,请说明理由.
分析 (1)根据AB∥FD,求出α的度数和∠EGB的度数求和得到答案;
(2)根据三角形外角的性质得到∠EGB=∠EFB+∠B,计算得到答案.
解答 解:(1)∵AB∥FD,
∴∠EGB=∠EFB=90°,
α=∠B=30°,
∠EGB+α=120°;
(2)不变,
∵∠BFD=α,
∴∠EFB=90°-α,
∴∠EGB=∠EFB+∠B=120°-α,
∴∠EGB+α=120°.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°和三角形外角的性质是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.
阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.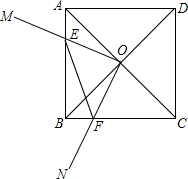 如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.
如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.