题目内容
14.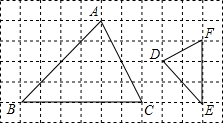 △ABC与△DEF在网格中的位置如图所示,如果每个小正方形的边长都是1.
△ABC与△DEF在网格中的位置如图所示,如果每个小正方形的边长都是1.(1)求$\frac{AB}{DE}$、$\frac{BC}{EF}$、$\frac{AC}{DF}$的值;
(2)求△ABC的周长与△DEF的周长的比;
(3)在AB、BC、AC、DE、EF、DF这六条线段中,指出其中三组成比例的线段.
分析 (1)根据网格和勾股定理求出AB、BC、AC、DE、EF、DF的长度即可解答;
(2)根据相似三角形的性质解答;
(3)根据成比例线段的概念找出成比例的线段.
解答 解:(1)AB=4$\sqrt{2}$,BC=6,AC=2$\sqrt{5}$,DE=2$\sqrt{2}$,EF=3,DF=$\sqrt{5}$,
∴$\frac{AB}{DE}$=2,$\frac{BC}{EF}$=2,$\frac{AC}{DF}$=2;
(2)∵$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$,
∴△ABC∽△DEF,
∴△ABC的周长与△DEF的周长的比为:2;
(3)$\frac{AB}{DE}$=$\frac{BC}{EF}$,AB、BC、DE、EF是成比例的线段;
$\frac{AB}{DE}$=$\frac{AC}{DF}$,AB、AC、DE、DF是成比例的线段;
$\frac{BC}{EF}$=$\frac{AC}{DF}$,AC、DE、EF、DF是成比例的线段.
点评 本题考查的是成比例线段、相似三角形的判定和性质、勾股定理的应用,根据格点求出线段的长度是解题的关键,相似三角形的周长之比等于相似比.

练习册系列答案
相关题目
5.已知A组有三个数:1,-2,3,B组有三个数:1,-$\sqrt{2}$,$\sqrt{3}$,若从B组任选两个数分别与A组的每个数相乘,共得到6个数,再把这6个数相加得到数m,则m>0的概率为( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
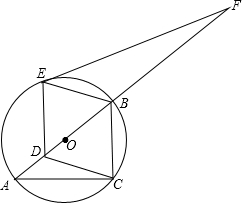 如图,点A,B,C在⊙O上,AB是⊙O的直径,AC=4,BC=3.
如图,点A,B,C在⊙O上,AB是⊙O的直径,AC=4,BC=3. 阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.
阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.