题目内容
13.有四张不透明的卡片,正面分别写有数字-1,-2,3,4,除正面的数字不同外,其余完全相同.将这4张卡片背面朝上洗匀后,先从中随机抽取一张,记这张卡片上的数字为k,再从余下的三张卡片中随机抽取一张,记其上面的数字为b.则使得一次函数y=kx+b的图象与两坐标轴围成的三角形面积不大于2的概率为$\frac{7}{12}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与使得一次函数y=kx+b的图象与两坐标轴围成的三角形面积不大于2的情况,再利用概率公式求解即可求得答案.
解答 解:画树状图得: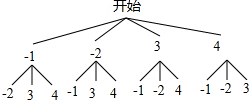
y=kx+b与两坐标轴的交点坐标为(-$\frac{b}{k}$,0)和(0,b),
∵一次函数y=kx+b的图象与两坐标轴围成的三角形面积不大于2,
∴$\frac{1}{2}$|-$\frac{b}{k}$|•|b|≤2,
即b2≥4k,或b2≤-4k,
由树状图知共有12种情况,满足b2≥4k,或b2≤-4k的有(-1,-2),(-2,-1),(3,-1),(3,-2),(4,-1),(4,-2),(4,3)7种情况,
∴P(一次函数y=kx+b的图象与两坐标轴围成的三角形面积不大于2)=$\frac{7}{12}$.
故答案为:$\frac{7}{12}$.
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
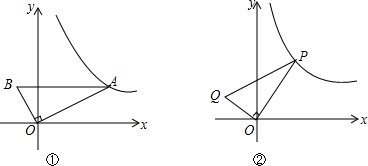
5.已知A组有三个数:1,-2,3,B组有三个数:1,-$\sqrt{2}$,$\sqrt{3}$,若从B组任选两个数分别与A组的每个数相乘,共得到6个数,再把这6个数相加得到数m,则m>0的概率为( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
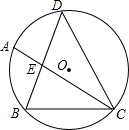 如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.
如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E. 在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,求△ABC的面积.
在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,求△ABC的面积.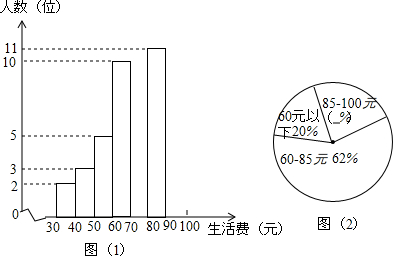
 阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.
阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.