如图所示.AB=AC.则C表示的数是1-$\sqrt{5}$．题目和参考答案——青夏教育精英家教网—

题目内容

4．

如图所示，AB=AC，则C表示的数是1-$\sqrt{5}$．

分析先根据勾股定理求出AB的长，即为AC的长，进而求出C表示的数．

解答解：∵图中直角三角形的两直角边为1，2，
∴斜边长为：$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
∴1和C之间的距离为$\sqrt{5}$．
∴点C表示的数为1-$\sqrt{5}$．
故答案为1-$\sqrt{5}$．

点评本题考查了实数与数轴，勾股定理，是基础题，熟记定理并求出AB的长是解题的关键．

练习册系列答案

相关题目

14．如果一个三角形的三个外角的度数之比是4：5：6，则这个三角形是（　　）

15．

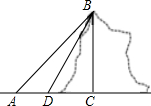如图，小明在A处用测角仪观测一座山的山顶B的仰角为45°，然后他前进了50米到达D处，观测B处的仰角为60°，求小山的高度BC（结果要求精确到1米，参考数据：$\sqrt{3}$≈1.7）

12．计算
（1）cos60°+$\frac{{\sqrt{2}}}{2}sin{45°}+\sqrt{3}tan{30°}$
（2）$\sqrt{{{sin}^2}{{60}°}-2sin{{60}°}+1}$-|1-tan60°|

19．郑老师想为七年级（1）班的同学购买学生用品，了解到某商店每个书包价格比每本词典多8元，用124元恰好可以买到3个书包和2本词典．
①每个书包和每本词典的价格各是多少元？
②郑老师计划用1000元为全班40位学生每人买一本词典，剩余的钱给6位家庭经济困难的同学每人买一个书包．问郑老师的1000元钱够吗？

9．解方程：
（1）2（x-3）-5（3-x）=21
（2）$\frac{2-x}{3}$-$\frac{3（x-1）}{2}$=4．

16．用配方法解方程x²-2x-6=0时，原方程应变形为（　　）

13．我们知道：对于任何实数x，①∵x²≥0，∴x²+1＞0；②∵${（x-\frac{1}{3}）^2}$≥0，∴${（x-\frac{1}{3}）^2}$+$\frac{1}{2}$＞0；模仿上述方法解答：求证：
（1）对于任何实数x，均有：2x²+4x+3＞0；
（2）不论x为何实数，多项式3x²-5x-1的值总大于2x²-4x-7的值．

14．满足-$\sqrt{5}$＜x＜$\sqrt{3}$的整数x是（　　）

试题分类