题目内容
12.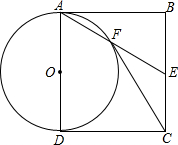 如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.
如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O交AE于点F,连接CF.(1)求证:CF与⊙O相切;
(2)若AD=2,F为AE的中点,求AB的长.
分析 (1)利用平行四边形的判定方法得出四边形OAEC是平行四边形,进而得出△ODC≌△OFC(SAS),求出OF⊥CF,进而得出答案;
(2)利用勾股定理得出DC的长,即可得出AB的长,
解答 (1)证明:如图所示:连接OF、OC,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO,
∴AO=$\frac{1}{2}$AD,EC=$\frac{1}{2}$BC,
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形,
∴AE∥OC,
∴∠DOC=∠OAF,∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠DOC=∠FOC,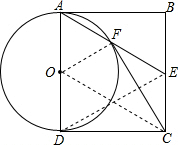
∵在△ODC和△OFC中
$\left\{\begin{array}{l}{OD=OF}\\{∠DOC=∠FOC}\\{OC=OC}\end{array}\right.$,
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与⊙O相切;
(2)解:如图所示:连接DE,
∵AO=DO,AF=EF,AD=2,
∴DE=20F=2,
∵E是BC的中点,
∴EC=1,
在Rt△DCE中,由勾股定理得:
DC=$\sqrt{D{E}^{2}-E{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AB=CD=$\sqrt{3}$.
点评 此题主要考查了全等三角形的判定与性质以及勾股定理和平行四边形的判定、切线的判定等知识,得出△ODC≌△OFC是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
2.小红爸爸上星期五买进某公司股票1000股,每股27元,下表为本周内每日该股的涨跌情况(单位:元).
(1)通过上表你认为星期三收盘时,每股是多少?
(2)该股票本周内每股最高是多少?最低是多少?
(3)小红爸爸买进一只股票是付了1.5%的手续费,卖出时还需付成交额1.5%的手续费和1%的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 该股票每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
(2)该股票本周内每股最高是多少?最低是多少?
(3)小红爸爸买进一只股票是付了1.5%的手续费,卖出时还需付成交额1.5%的手续费和1%的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?
20.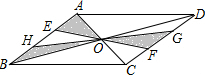 如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
 如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )
如图,?ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向?ABCD内部投掷飞镖(每次均落在?ABCD内,且落在?ABCD内任何一点的机会均等)恰好落在阴影区域的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
8.如图,将一张正六边形纸片的阴影部分剪下,拼成一个四边形,若拼成的四边形的面积为2a,则纸片的剩余部分的面积为 ( )
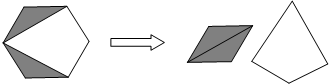

| A. | 5a | B. | 4a | C. | 3a | D. | 2a |
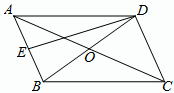 如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个.
如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个.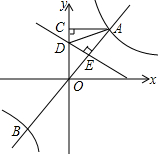 如图,过原点O的直线AB与反比例函数y=$\frac{k}{x}$(k>0)的图象交于A、B两点,点B坐标为(-2,m),过点A作AC⊥y轴于点C,OA的垂直平分线DE交OC于点D,交AB于点E.若△ACD的周长为5,则k的值为6.
如图,过原点O的直线AB与反比例函数y=$\frac{k}{x}$(k>0)的图象交于A、B两点,点B坐标为(-2,m),过点A作AC⊥y轴于点C,OA的垂直平分线DE交OC于点D,交AB于点E.若△ACD的周长为5,则k的值为6. 如图,Rt△ABC的∠A的平分线与过斜边中点M的垂线交于点D,求证:MA=MD.
如图,Rt△ABC的∠A的平分线与过斜边中点M的垂线交于点D,求证:MA=MD.