题目内容
17.已知点A(x1,y1),B(x2,y2)是反比例函数y=-$\frac{2}{x}$的图象上的两点,若x1<0<x2,则y1>y2.(填“>”或“<”或“=”)
分析 根据反比例函数图象上点的坐标特征得到y1=-$\frac{2}{{x}_{1}}$,y2=-$\frac{2}{{x}_{2}}$,然后利用x1与x2的大小关系比较y1与y2的大小.
解答 解:∵点A(x1,y1),B(x2,y2)是反比例函数y=-$\frac{2}{x}$的图象上的两点,
∴y1=-$\frac{2}{{x}_{1}}$,y2=-$\frac{2}{{x}_{2}}$,
而x1<0<x2,
∴y1>y2.
故答案为>.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
8.如图,将一张正六边形纸片的阴影部分剪下,拼成一个四边形,若拼成的四边形的面积为2a,则纸片的剩余部分的面积为 ( )
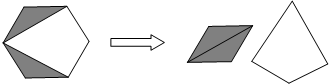

| A. | 5a | B. | 4a | C. | 3a | D. | 2a |
12.下列运算中,错误的是( )
| A. | (-$\sqrt{2}$)2=2 | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
2.下列命题中,假命题是( )
| A. | 方差是衡量一组数据波动大小的统计量 | |
| B. | 影响鞋店进货时决策的主要统计量是众数 | |
| C. | 对角线互相垂直且相等的四边形是正方形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
9.我国第六次全国人口普查数据显示,居住在城镇的人口总数大约为6 6600 0000人,用科学记数法表示为( )
| A. | 66.6×107 | B. | 6.66×108 | C. | 6.66×107 | D. | 0.666×109 |
 如图,Rt△ABC的∠A的平分线与过斜边中点M的垂线交于点D,求证:MA=MD.
如图,Rt△ABC的∠A的平分线与过斜边中点M的垂线交于点D,求证:MA=MD. 如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.
如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.


