题目内容
18.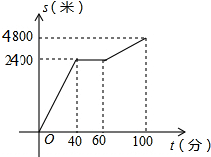 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )| A. | 小明中途休息用了20分钟 | |
| B. | 小明休息前爬山的速度为每分钟60米 | |
| C. | 小明在上述过程中所走路程为7200米 | |
| D. | 小明休息前后爬山的平均速度相等 |
分析 根据函数图象可知,小明40分钟爬山2400米,40~60分钟休息,60~100分钟爬山(4800-2400)米,爬山的总路程为4800米,根据路程、速度、时间之间的关系进行解答即可.
解答 解:A、小明中途休息的时间是:60-40=20分钟,故本选项正确;
B、小明休息前爬山的速度为$\frac{2400}{40}$=60(米/分钟),故本选项正确;
C、小明在上述过程中所走路程为4800米,故本选项错误;’
D、因为小明休息后爬山的速度是$\frac{4800-2400}{100-60}$=60(米/分钟),所以小明休息前后爬山的平均速度相等,故本选项正确;
故选C.
点评 本题考查了函数图象,读懂函数图象,从图象中获取必要的信息是解决本题的关键.

练习册系列答案
相关题目
6. 如图,直线a∥b,∠1=130°,∠2=60°,则∠3=( )
如图,直线a∥b,∠1=130°,∠2=60°,则∠3=( )
 如图,直线a∥b,∠1=130°,∠2=60°,则∠3=( )
如图,直线a∥b,∠1=130°,∠2=60°,则∠3=( )| A. | 95° | B. | 100° | C. | 105° | D. | 110° |
7. 如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )
如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )
 如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )
如图,AB∥CD,EF交AB于点E,交CD于点F,若EG平分∠BEF交CD于点G,EF平分∠AEG,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
3.某个函数自变量的取值范围是x≥-1,则这个函数的表达式为( )
| A. | y=x+1 | B. | y=x2+1 | C. | y=$\sqrt{x+1}$ | D. | y=$\frac{1}{x+1}$ |
10.若等腰三角形的一边长为6,另两边长分别是关于x的方程x2-(k+5)x+3k+6=0的两个根,则k的值是( )
| A. | -1或4 | B. | -1 | C. | 1或4 | D. | 4 |
7.下列说法正确的是( )
| A. | 若ab=0,则点P(a,b)表示原点 | B. | 坐标轴上的点不属于任何象限 | ||
| C. | 已知点A(3,-2),则它到x轴的距离为3 | D. | 点(1,-a2)在第四象限 |
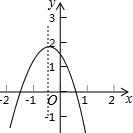 已知抛物线y=ax2+bx+c的图象如图所示,则①abc>0;②b2-4ac>0;③a+b+c<0;④a-b+c<0,正确的有①②③(填序号).
已知抛物线y=ax2+bx+c的图象如图所示,则①abc>0;②b2-4ac>0;③a+b+c<0;④a-b+c<0,正确的有①②③(填序号). 如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )
如图直线y=$\frac{1}{2}$x+1与x轴交于点A,与双曲线y=$\frac{k}{x}$(x>0)交于点P,过点P作PC⊥x轴于点C,且PC=2,则k的值为( )