题目内容
13.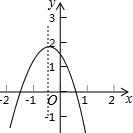 已知抛物线y=ax2+bx+c的图象如图所示,则①abc>0;②b2-4ac>0;③a+b+c<0;④a-b+c<0,正确的有①②③(填序号).
已知抛物线y=ax2+bx+c的图象如图所示,则①abc>0;②b2-4ac>0;③a+b+c<0;④a-b+c<0,正确的有①②③(填序号).
分析 根据抛物线的开口方向可确定出a范围,根据对称轴方程可确定出b的范围,由抛物线与y轴交点可得到C的范围,故此可判断①,由抛物线与x轴的交点个数可判断②,根据x=1和x=-1时,对应函数值可判断③和④.
解答 解:∵抛物线开口向下,
∴a<0.
又∵x=-$\frac{b}{2a}$<0,
∴b<0.
∵当x=0,y=c,
∴c>0.
∴abc>0.
∴①正确.
∵抛物线与x轴有两个交点,
∴b2-4ac>0.
故②正确.
当x=1时,y=a+b+c<0,故③正确;
当x=-1时,y=a-b+c>0,故④错误.
故答案为:①②③.
点评 本题主要考查的是二次函数的图象与系数的关系,熟练掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{5}$-$\sqrt{4}$=1 | C. | $\sqrt{(3-π)^{2}}$=3-π | D. | $\root{3}{{2}^{3}}$=2 |
1.某部队为了测量一批新制造的炮弹的杀伤半径,从中抽查了50枚炮弹,它们的杀伤半径(单位:千米)如表:
这批炮弹的平均杀伤半径是多少千米?
| 杀伤半径 | 20≤x<40 | 40≤x<60 | 60≤x<80 | 80≤x<100 |
| 数量 | 8 | 12 | 25 | 5 |
8.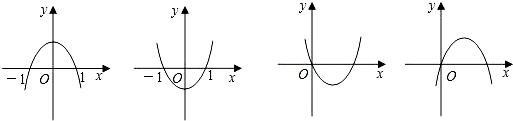 设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
 设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )| A. | 6或-1 | B. | -6或 1 | C. | 6 | D. | -1 |
18.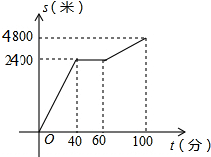 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )
 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )| A. | 小明中途休息用了20分钟 | |
| B. | 小明休息前爬山的速度为每分钟60米 | |
| C. | 小明在上述过程中所走路程为7200米 | |
| D. | 小明休息前后爬山的平均速度相等 |
2.对于函数y=-2x+1,下列结论正确的是( )
| A. | 它的图象必经过点(-1,2) | B. | 它的图象经过第一、二、三象限 | ||
| C. | 当x>1时,y<0 | D. | y的值随x值的增大而增大 |
 如图,在数轴上点A表示的实数是$\sqrt{5}$.
如图,在数轴上点A表示的实数是$\sqrt{5}$.