题目内容
10.计算:(1)(132-122)${\;}^{\frac{1}{2}}$;
(2)(2${\;}^{\frac{1}{2}}$+3${\;}^{\frac{1}{2}}$)2.
分析 (1)先利用平方差公式,再运用分数指数幂的定义求解,
(2)先利用分数指数幂的定义化简,再运用完全平方公式求解即可.
解答 解:(1)(132-122)${\;}^{\frac{1}{2}}$
=$[(13+12)(13-12)]^{\frac{1}{2}}$
=$2{5}^{\frac{1}{2}}$
=5;
(2)(2${\;}^{\frac{1}{2}}$+3${\;}^{\frac{1}{2}}$)2
=($\sqrt{2}$+$\sqrt{3}$)2
=5+2$\sqrt{6}$.
点评 本题主要考查了分数指数幂,解题的关键是熟记分数指数幂的定义.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5. 如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为( )
如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为( )
 如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为( )
如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为( )| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 3 |
15.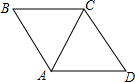 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )| A. | 绕点A顺时针旋转60°得到的 | B. | 绕点A顺时针旋转120°得到的 | ||
| C. | 绕点C顺时针旋转60°得到的 | D. | 绕点C顺时针旋转120°得到的 |
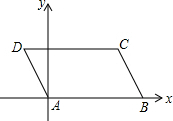 在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).
在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).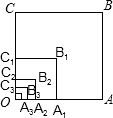 如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的$\frac{1}{2}$,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的$\frac{1}{2}$,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的$\frac{1}{2}$,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=16.
如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的$\frac{1}{2}$,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的$\frac{1}{2}$,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的$\frac{1}{2}$,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=16.