题目内容
2. 如图,已知AE=CF,∠AFD=∠CEB,那么添加一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠AFD=∠CEB,那么添加一个条件后,仍无法判定△ADF≌△CBE的是( )| A. | AD=CB | B. | ∠A=∠C | C. | BE=DF | D. | AD∥BC |
分析 根据全等三角形的判定方法依次进行判断即可.
解答 解:
∵AE=CF,
∴AF=CE,且∠AFD=∠CEB,
当AD=CB时,在△ADF和△CBE中,满足的是SSA,故A不能判定;
当∠A=∠C时,在△ADF和△CBE中,满足ASA,故B可以判定;
当BE=DF时,在△ADF和△CBE中,满足SAS,故C可以判定;
当AD∥BC时,可得∠A=∠C,同选项B,故D可以判定;
故选A.
点评 本题主要考查三角形全等的判定方法,掌握全等三角形的五种判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
13. 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )| A. | 5 cm | B. | 10 cm | C. | 20 cm | D. | 40 cm |
10.下列给出4个命题:
①内错角相等;
②对顶角相等;
③对于任意实数x,代数式x2-6x+10总是正数;
④若三条线段a、b、c满足a+b>c,则三条线段a、b、c一定能组成三角形.
其中正确命题的个数是( )
①内错角相等;
②对顶角相等;
③对于任意实数x,代数式x2-6x+10总是正数;
④若三条线段a、b、c满足a+b>c,则三条线段a、b、c一定能组成三角形.
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.点P反比例函数y=-$\frac{2\sqrt{3}}{x}$的图象上,过点P分别作坐标轴的垂线段PM、PN,则四边形OMPN的面积=( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 1 |
11. 如图OA⊥OB,若∠BOC=40°,则∠AOC的度数是( )
如图OA⊥OB,若∠BOC=40°,则∠AOC的度数是( )
 如图OA⊥OB,若∠BOC=40°,则∠AOC的度数是( )
如图OA⊥OB,若∠BOC=40°,则∠AOC的度数是( )| A. | 20° | B. | 40° | C. | 50° | D. | 60° |
12.反比例函数y=$\frac{1-5m}{x}$图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,y1<y2,则m的取值范围是( )
| A. | m>$\frac{1}{5}$ | B. | m<$\frac{1}{5}$ | C. | m≥$\frac{1}{5}$ | D. | m≤$\frac{1}{5}$ |

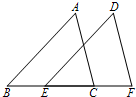 如图,△DEF是将△ABC沿射线BC的方向平移后得到的.若BC=5,EC=3,则CF的长为( )
如图,△DEF是将△ABC沿射线BC的方向平移后得到的.若BC=5,EC=3,则CF的长为( )