题目内容
5.李爷爷家有一块三角形的花圃,他准备将其分成面积相等的四个部分,分别种上四种不同的花,请你帮李爷爷设计方案.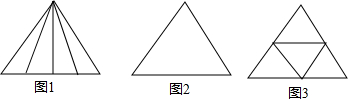
(1)如图1是王明设计的方案,取其中一边的四等分点,将三角形分成四个面积相等的三角形,请你在图2中设计一种与王明不同的方案;
(2)如图3是李昊同学设计的方案,取三边的中点,然后依次连接,将原图形分成四个三角形,请你说出这种方案的合理性.
分析 (1)三角形的中线将三角形分割为两个面积相等的三角形,从而可进行分割;
(2)依据相似三角形的面积比等于相似比的平方进行证明即可.
解答 解:(1)如图2所示:取三边的中点.
(2)合理:
理由:如图3所示:
∵点D、E分别为AB、AC的中点,
∴DE是三角形的中线.
∴DE∥BC,DE=$\frac{1}{2}$BC.
∴△ADE∽△ABC.
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=(\frac{DE}{BC})^{2}=\frac{1}{4}$.
∴${S}_{△ADE}=\frac{1}{4}$S△ABC.
同理:${S}_{△BDF}=\frac{1}{4}{S}_{△ABC}$,${S}_{△CEF}=\frac{1}{4}{S}_{△ABC}$.
∴${S}_{△DEF}=\frac{1}{4}{S}_{△ABC}$.
∴S△ADE=S△BDF=S△CEF=S△DEF.
点评 本题主要考查的是作图-应用与设计作图,证得△ADE∽△ABC,然后依据相似三角形的性质得到${S}_{△ADE}=\frac{1}{4}$S△ABC是解题的关键.

练习册系列答案
相关题目
15.已知|x-2|+|y+3|=0,则x-y的值是( )
| A. | -5 | B. | 5 | C. | 4 | D. | -8 |
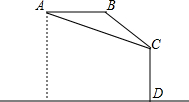 如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度.
如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度.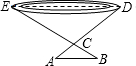 如图,为了测量一池塘的宽DE,在岸边找一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE,交EC的延长线于B,测得AB=6m,求池塘的宽DE.
如图,为了测量一池塘的宽DE,在岸边找一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE,交EC的延长线于B,测得AB=6m,求池塘的宽DE. 如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.
如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF. 如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,
如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H, 如图所示,△ABC和△CDE是等边三角形,E是AC延长线上一点,M是AD的中点,N是BE的中点.试说明:△CMN是等边三角形.
如图所示,△ABC和△CDE是等边三角形,E是AC延长线上一点,M是AD的中点,N是BE的中点.试说明:△CMN是等边三角形.