题目内容
12. 如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )| A. | 2cm2 | B. | 1cm2 | C. | 0.5cm2 | D. | 0.25cm2 |
分析 首先根据E为AD的中点,可得BE、CE分别是△ABD、△ACD的中线,然后根据三角形的中线把三角形分成面积相同的两部分,可得S△BDE=$\frac{1}{2}$S△ABD,S△CDE=$\frac{1}{2}$S△ABD,所以S△BEC=$\frac{1}{2}$S△ABC,据此求出S△BEC的值为多少即可.
解答 解:∵E为AD的中点,
∴BE、CE分别是△ABD、△ACD的中线,
∴S△BDE=$\frac{1}{2}$S△ABD、S△CDE=$\frac{1}{2}$S△ACD,
∴S△BEC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×4=2(cm2),
即S△BEC的值为2cm2.
故选:A.
点评 (1)此题主要考查了三角形的面积的求法,要熟练掌握,解答此题的关键是要明确:两个三角形的高一定时,面积和底成正比.
(2)此题还考查了三角形的中线的性质和应用,解答此题的关键是要明确:三角形的中线把三角形分成面积相同的两部分.

练习册系列答案
相关题目
1.“扬州是我家,爱护靠大家”.自我市开展整治“六乱”行动以来,我市学生更加自觉遵守交通规则.某校学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为$\frac{1}{3}$,遇到黄灯的概率为$\frac{1}{9}$,那么他遇到绿灯的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
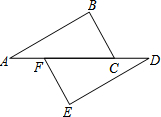 如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠A=∠D,AB=DE,BC∥EF,求证:AF=DC.
如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且∠A=∠D,AB=DE,BC∥EF,求证:AF=DC.