题目内容
 如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点F,延长CE到点G,使CG=AB,若∠BCE=45°,求证:点F、点G关于AB对称.
如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点F,延长CE到点G,使CG=AB,若∠BCE=45°,求证:点F、点G关于AB对称.考点:全等三角形的判定与性质,轴对称的性质
专题:证明题
分析:连接AF,由BD⊥AC,CE⊥AB得到一对角为直角,利用两对角相等的三角形相似得到三角形ABD与三角形ACE相似,得到∠ACE=∠ABD,再由一对直角相等,且夹边BE=CE,利用ASA得到三角形BEF与三角形ACE全等,利用全等三角形对应边相等得到AE=EF,再由AE=GE,等量代换得到GE=EF,再由AB垂直于GF,即可得到点F、点G关于AB对称.
解答: 证明:连接AF,
证明:连接AF,
∵BD⊥AC,CE⊥AB,
∴∠BEC=∠AEG=90°,
∵∠AEC=∠ADB=90°,∠CAE=∠BAD(公共角相等),
∴△ACE∽△ABD,
∴∠ABD=∠ACE,
∵∠BCG=45°,
∴△AEG与△EBC都为等腰直角三角形,
∴AE=GE,BE=CE,
在△BEF和△CEA中,
,
∴△BEF≌△CEA(ASA),
∴EF=EA,
又∵GE=AE,
∴GE=EF,
又∵CE⊥AB,
∴F、G关于AB对称.
 证明:连接AF,
证明:连接AF,∵BD⊥AC,CE⊥AB,
∴∠BEC=∠AEG=90°,
∵∠AEC=∠ADB=90°,∠CAE=∠BAD(公共角相等),
∴△ACE∽△ABD,
∴∠ABD=∠ACE,
∵∠BCG=45°,
∴△AEG与△EBC都为等腰直角三角形,
∴AE=GE,BE=CE,
在△BEF和△CEA中,
|
∴△BEF≌△CEA(ASA),
∴EF=EA,
又∵GE=AE,
∴GE=EF,
又∵CE⊥AB,
∴F、G关于AB对称.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,与∠1成内错角的角有( )
如图,与∠1成内错角的角有( )| A、2个 | B、3个 | C、4个 | D、5个 |

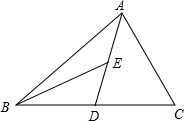 如图,AD为△ABC的中线,BE为△ABD的角平分线.
如图,AD为△ABC的中线,BE为△ABD的角平分线. 如图,已知弦AB、CD相交于P点,且∠AOC=44°,∠BOD=46°.则∠APC的度数是
如图,已知弦AB、CD相交于P点,且∠AOC=44°,∠BOD=46°.则∠APC的度数是