题目内容
20.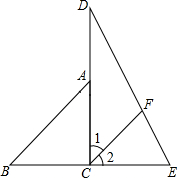 将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
分析 先根据直角三角板的性质得出∠BAC=45°,再由角平分线的性质得出∠1=45°,进而可得出结论.
解答 解:CF∥AB.
∵图中是一副直角三角板,
∴∠BAC=45°.
∵CF平分∠DCE,
∴∠1=45°,
∴CF∥AB.
点评 本题考查的是平行线的判定,熟知直角三角板各内角的度数是解答此题的关键.

练习册系列答案
相关题目
15.若|3x+2y-4|+27(5x+6y)2=0,则x,y的值分别是( )
| A. | $\left\{\begin{array}{l}{x=6}\\{y=-5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-\frac{5}{2}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=-\frac{11}{2}}\end{array}\right.$ |
5.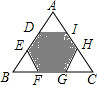 如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
 如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )
如图,正六边形DEFGHI的顶点分别在等边△ABC各边上,则$\frac{{S}_{阴影}}{{S}_{等边△ABC}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
12. 如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )
 如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{BC}$,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )| A. | $\frac{5}{3}π-2\sqrt{3}$ | B. | $\frac{5}{3}π+2\sqrt{3}$ | C. | 2$\sqrt{3}-\frac{5}{3}π$ | D. | $\sqrt{3}+\frac{5}{3}π$ |
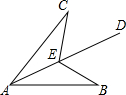 如图,AD平分∠BAC,点E在射线AD上,∠BED=∠CED,求证:AB=AC.
如图,AD平分∠BAC,点E在射线AD上,∠BED=∠CED,求证:AB=AC.