题目内容
 如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=
如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=| 3 |
| 4 |
(1)求抛物线的函数解析式;
(2)直线m与⊙C相切于点A,交y轴于点D,动点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,当PQ⊥AD时,求运动时间t的值;
(3)将抛物线向上平移k个单位(k可以为负数,即向下平移-k个单位)若平移后的抛物线与四边形ODAB的四边恰好只有两个公共点时,求实数k的取值范围.
考点:二次函数综合题
专题:
分析:(1)利用待定系数法求二次函数解析式解析式即可;
(2)连接AC交OB于E,作OF⊥AD于F,得出m∥OB,进而求出OD,OF的长,进而利用勾股定理得出DF的长;
(3)利用抛物线y=
x2-2x+k与直线AD只有一个公共点,利用一元二次方程根的判别式得出k的值,再利用抛物线y=
x2-2x+k与直线OB只有一个公共点得出k的值,进而得出k的取值范围,若抛物线y=
x2-2x+k过D(0,-3)点,则k=-3,进而得出k的取值范围.
(2)连接AC交OB于E,作OF⊥AD于F,得出m∥OB,进而求出OD,OF的长,进而利用勾股定理得出DF的长;
(3)利用抛物线y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)将点A(4,0)和点(-2,6)的坐标代入y=ax2+bx中,得方程组,
解得
,
故抛物线的解析式为y=
x2-2x.
(2)如图所示,连接AC交OB于E.作OF⊥AD于F,
∵直线m切⊙C于点A,
∴AC⊥m.
∵弦AB=AO,
∴
=
.
∴AC⊥OB,
∴m∥OB.
∴∠OAD=∠AOB.
又∵PQ⊥AD,
∴四边形OFQP是矩形,
∵OA=4,tan∠AOB=
,
∴OD=OA•tan∠OAD=4×
=3.
则OF=OA•sin∠OAD=4×
=2.4.
t秒时,OP=t,DQ=2t,
若PQ⊥AD,则 FQ=OP=t.DF=DQ-FQ=t.
∴△ODF中,t=DF=
=1.8(秒);
(3)∵原抛物线为y=
x2-2x,
∴平移后的抛物线为:y=
x2-2x+k,
∵A(4,0),D(0,-3),
设直线AD的解析式为y=ex+d
则
,
解得:
故直线AD的解析式为y=
x-3,
若抛物线y=
x2-2x+k与直线AD只有一个公共点,则由
,
得:
x2-
x+k+3=0,
故△=(
)2-4×
(k+3)=0,
解得:k=
,
若抛物线y=
x2-2x+k与直线OB只有一个公共点,则
由
,得
x2-
x+k=0,
故△=(
)2-4×
k=0,
解得:k=
,
若抛物线y=
x2-2x+k过D(0,-3)点,则k=-3,
综上所述,当平移后的抛物线与四边形ODAB的四边恰好只有两个公共点时,
实数k的取值范围是:
<k<
或-3<k<0.
|
解得
|
故抛物线的解析式为y=
| 1 |
| 2 |
(2)如图所示,连接AC交OB于E.作OF⊥AD于F,
∵直线m切⊙C于点A,

∴AC⊥m.
∵弦AB=AO,
∴
 |
| OA |
 |
| AB |
∴AC⊥OB,
∴m∥OB.
∴∠OAD=∠AOB.
又∵PQ⊥AD,
∴四边形OFQP是矩形,
∵OA=4,tan∠AOB=
| 3 |
| 4 |
∴OD=OA•tan∠OAD=4×
| 3 |
| 4 |
则OF=OA•sin∠OAD=4×
| 3 |
| 5 |
t秒时,OP=t,DQ=2t,
若PQ⊥AD,则 FQ=OP=t.DF=DQ-FQ=t.
∴△ODF中,t=DF=
| OD2-OF2 |
(3)∵原抛物线为y=
| 1 |
| 2 |
∴平移后的抛物线为:y=
| 1 |
| 2 |
∵A(4,0),D(0,-3),
设直线AD的解析式为y=ex+d
则
|
解得:
|
故直线AD的解析式为y=
| 3 |
| 4 |
若抛物线y=
| 1 |
| 2 |
|
得:
| 1 |
| 2 |
| 11 |
| 4 |
故△=(
| 11 |
| 4 |
| 1 |
| 2 |
解得:k=
| 25 |
| 32 |
若抛物线y=
| 1 |
| 2 |
由
|
| 1 |
| 2 |
| 11 |
| 4 |
故△=(
| 11 |
| 4 |
| 1 |
| 2 |
解得:k=
| 121 |
| 32 |
若抛物线y=
| 1 |
| 2 |
综上所述,当平移后的抛物线与四边形ODAB的四边恰好只有两个公共点时,
实数k的取值范围是:
| 25 |
| 32 |
| 121 |
| 32 |
点评:此题主要考查了二次函数的综合应用以及垂径定理的推论和勾股定理等知识,根据切线的性质以及锐角三角函数关系得出OF的长是解题关键.

练习册系列答案
相关题目
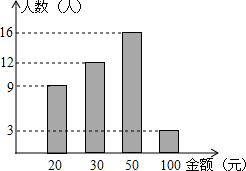 春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.
春节将至,某中学八年级(1)班共有40名同学参加了“春节送温暖”捐款活动.活动结束后,生活委员小林将捐款情况进行了统计,并绘制成如右的统计图.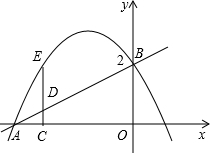 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线