题目内容
11. 如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=5或10,△ABC与△APQ全等.
如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=5或10,△ABC与△APQ全等.
分析 分两种情况:①当AP=BC=5时;②当AP=CA=10时;由HL证明Rt△ABC≌Rt△PQA(HL);即可得出结果.
解答 解:∵AX⊥AC,
∴∠PAQ=90°,
∴∠C=∠PAQ=90,
分两种情况:
①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,$\left\{\begin{array}{l}{AB=PQ}\\{BC=AP}\end{array}\right.$,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在△ABC和△PQA中,$\left\{\begin{array}{l}{AB=PQ}\\{AP=AC}\end{array}\right.$,
∴Rt△ABC≌Rt△PQA(HL);
综上所述:当点P运动到AP=5或10时,△ABC与△APQ全等;
故答案为:5或10.
点评 本题考查了直角三角形全等的判定方法;熟练掌握直角三角形全等的判定方法,本题需要分类讨论,难度适中.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
16.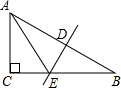 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )
 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )| A. | DE=EC | B. | ∠B=∠CAE | C. | ∠DEA=∠CEA | D. | BE=AC |
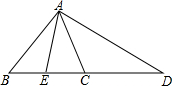 如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.
如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.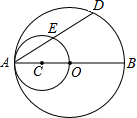 如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E.
如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E.
 已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.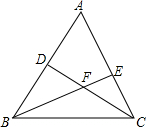 如图,∠A=70°,∠ABE=30°,∠ACD=25°,∠ACD=25°,则∠BDC=95度,∠BEC=100度,∠BFC=125度.
如图,∠A=70°,∠ABE=30°,∠ACD=25°,∠ACD=25°,则∠BDC=95度,∠BEC=100度,∠BFC=125度.