题目内容
6．
已知：如图，BD、CE是△ABC的高，M为BC的中点．试说明点B、C、D、E在以点M为圆心的同一个圆上．
分析 分别连接ME、MF，根据直角三角形中，斜边上的中线等于斜边的一半可得到ME=MD=MC=MB，可证得结论．
解答 
证明：连接ME、MD，
∵BD、CE分别是△ABC的高，M为BC的中点，
∴ME=MD=MC=MB=$\frac{1}{2}$BC，
∴点B、C、D、E在以点M为圆心的同一圆上．
点评 本题主要考查直角三角形的性质，根据直角三角形中斜边上的中线等于斜边的一半得到ME=MF=MC=MB是解题的关键．
练习册系列答案
相关题目
把两根钢条A′B、AB′的中点连在一起，可以做成一个测量工件内槽宽工具（卡钳）．如图，若测得AB=5厘米，则槽为5厘米．
如图，∠C=90°，AC=10，BC=5，AX⊥AC，点P和点Q从A点出发，分别在线段AC和射线AX上运动，且AB=PQ，当点P运动到AP=5或10，△ABC与△APQ全等．
如图，E、F分别为线段AC上的两个动点，且DE⊥AC于E点，BF⊥AC于F点，若AB=CD，AF=CE，BD交AC于M点．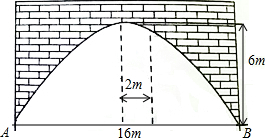
如图，有一个抛物线型拱桥，桥洞离水面的最大高度为6m，跨度为16m，请建立适当的直角坐标系． 
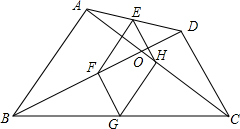如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD，BD，BC，AC的中点．