题目内容
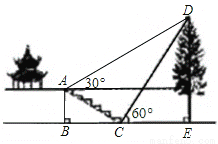
如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度．他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2米，台阶AC的坡度为1：
（即AB：BC=1：），且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（测倾器的高度忽略不计）．
【解析】
因为直角三角形ABC中，BC=，AB=4， 所以BC=4，设DF=x，
在直角三角形AFD中，
,
在直角三角形DCE中，
,
所以
所以DE=米。
【解析】试题分析：由于AF⊥AB，则四边形ABEF为矩形，设DE=x，在Rt△CDE中，CE═==，在Rt△ABC中，得到，求出BC，在Rt△AFD中，求出AF，由AF=BC+CE即可求出x的长．...
如图，将二次函数y=31x2-999x+892的图形画在坐标平面上，判断方程31x2-999x+892=0的两根，下列叙述何者正确（ ）
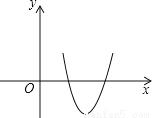
A. 两根相异，且均为正根
B. 两根相异，且只有一个正根
C. 两根相同，且为正根
D. 两根相同，且为负根
A
【解析】∵二次函数y=31x2-999x+892的图象与x轴有两个交点，且与x轴的正半轴相交，
∴方程31x2-999x+892=0有两个正实根．
故选：A． 有两条或两条以上对称轴的轴对称图形是（ ）
A. 等腰三角形 B. 角 C. 等边三角形 D. 锐角三角形
C
【解析】A.等腰三角形只有一条对称轴；
B.角也只有一条对称轴，是角平分线所在的直线；
C.等边三角形有三条对称轴；
D.锐角三角形的对称轴数量不确定.
故选：C 在△ABC中，∠B＝40°，∠C＝70°，则△ABC中是 三角形
等腰
【解析】本题考查的是三角形的分类。∠C=180°-40°-70°＝70°，所以∠A＝∠C=70°故为等腰三角形。 如图，MN表示某引水工程的一段设计路线，从点M到点N的走向为北偏西30°，在点M的北偏西60°方向上有一点A，以点A为圆心，以500米为半径的圆形区域为居民区，取MN上另一点B，测得BA的方向为北偏西75°．已知MB=400米，若不改变方向，则输水路线是否会穿过居民区？请通过计算说明理由．（参考数据：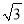 
≈1.732）
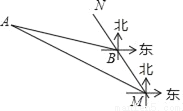
不会穿过居民区，理由见解析.
【解析】试题分析：要判断输水路线是否会穿过居民区，即要比较点A到MN的距离与500的大小，要求点A到MN的距离，作AD⊥MN交MN于点D，设AD=x，不难表示出DM=x+400，再由tan∠AMD==列出方程，解出x，比较x与500的大小，若x＞500，则不会穿过居民区；若x≤500，则会穿过居民区.
试题解析：
【解析】
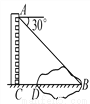
过A作AD⊥MN于点D，... 如图，某同学在楼房的A处测得荷塘的一端B处的俯角为30°，荷塘另一端D与点C、B在同一条直线上．已知AC＝32米，CD＝16米，则荷塘宽BD为________米(取
≈1.73，结果保留整数)．
39
【解析】试题分析：根据题意可得：∠B=30°，在Rt△ABC中，tan∠B=tan30°=，则BC=32≈55米，则BD=BC-CD=55-16=39米． 某工厂在生产过程中要消耗大量电能，消耗每千度电产生利润与电价是一次函数关系，经过测算，工厂每千度电产生利润y（元/千度））与电价x（元/千度）的函数图象如图：
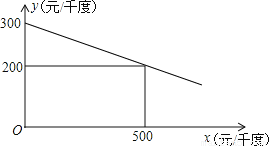
（1）当电价为600元/千度时，工厂消耗每千度电产生利润是多少？
（2）为了实现节能减排目标，有关部门规定，该厂电价x（元/千度）与每天用电量m（千度）的函数关系为x=10m+500，且该工厂每天用电量不超过60千度，为了获得最大利润，工厂每天应安排使用多少度电？工厂每天消耗电产生利润最大是多少元？
（1）工厂消耗每千度电产生利润是180元（2）当工厂每天消耗50千度电时，工厂每天消耗电产生利润为5000元
【解析】试题分析：（1）设y=kx+b（k≠0），利用待定系数法求一次函数解析式解答即可；
（2）根据利润=每天的用电量×每千度电产生利润y，然后整理得到W与m的关系式，再根据二次函数的最值问题解答．
【解析】
（1）设工厂每千度电产生利润y（元/千度）与电价x（元/千... 如图，二次函数y= -x2-2x的图象与x轴交于点A、O，在抛物线上有一点P，满足
S△AOP=3，则点P的坐标是（ ）
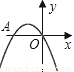
A. （-3，-3） B. （1，-3） C. （-3，-3）或（-3，1） D. （-3，-3）或（1，-3）
D
【解析】分析：根据抛物线的解析式，即可确定点A的坐标，由于OA是定长，根据△AOP的面积即可确定P点纵坐标的绝对值，将其代入抛物线的解析式中，即可求得P点的坐标．
解答：【解析】
抛物线的解析式中，令y=0，得：-x2-2x=0，解得x=0，x=-2；
∴A（-2，0），OA=2；
∵S△AOP=OA?|yP|=3，∴|yP|=3；
当P点纵坐标为3时，-x2-... 如图，对称轴平行于y轴的抛物线与x轴交于(1，0)、(3，0)两点，则它的对称轴为____________________．
直线x＝2
【解析】试题分析：当两点到对称轴距离相等时，则所对应的函数值相等，则二次函数的对称轴为：x==2.