题目内容
2.(1)设n表示任意一个整数,则用含有n的代数式表示任意一个偶数为2n,用含有n的代数式表示任意一个奇数为2n-1;(答案直接填在题中横线上)(2)用举例验证的方案探索:任意两个整数的和与这两个数的差是否同时为奇数或同时为偶数?你的结论是是;(填“是”或“否”,答案直接填在题中横线上)
(3)设a、b是任意的两个整数,试用“用字母表示数”的方法并分情况来说明a+b和a-b是否“同时为奇数”或“同时为偶数”?并进一步得出一般性的结论.
例:①若a、b都是偶数,设a=2m,b=2n,则a+b=2m+2n=2(m+n);a-b=2m-2n=2(m-n);
此时a+b和a-b同时为偶数.
请你仿照以上的方法并考虑其余所有可能的情况加以计算和说明;
(4)以(3)的结论为基础进一步探索:若a、b是任意的两个整数,那么-a+b、-a-b、a+b、a-b是否“同时为奇数”或“同时为偶数”?
(5)应用第(2)、(3)、(4)的结论完成:在2016个自然数1,2,3,…,2015,2016的每一个数的前面任意添加“+”或“-”,则其代数和一定是偶数.(填“奇数”或“偶数”,答案直接填在题中横线上)
分析 (1)根据奇数与偶数的定义写出即可;
(2)任意两个整数的和与这两个数的差是同时为奇数或同时为偶数;
(3)分①设a=2m,b=2n,②设a=2m,b=2n+1,③设a=2m+1,b=2n,④设a=2m+1,b=2n+1四种情况讨论可证明结论;
(4)由(3)的结论得出;
(5)应用第(2)、(3)、(4)的结论完成.
解答 解:(1)用含有n的代数式表示任意一个偶数为2n,用含有n的代数式表示任意一个奇数为2n+1或2n-1(奇数的表达式写出一个即可);
(2)任意两个整数的和与这两个数的差是同时为奇数或同时为偶数;
(3)②设a=2m,b=2n+1,
则:a+b=2m+2n+1=2(m+n)+1a-b=2m-(2n+1)=2(m-n)-1,
此时a+b和a-b同时为奇数;
③设a=2m+1,b=2n,
则:a+b=2m+1+2n=2(m+n)+1a-b=2m+1-2n=2(m-n)+1,
此时a+b和a-b同时为奇数;
④设a=2m+1,b=2n+1,
则:a+b=2m+1+2n+1=2(m+n+1)a-b=(2m+1)-(2n+1)=2(m-n),
此时a+b和a-b同时为偶数,
由此可见:a+b和a-b要么同时为奇数,要么同时为偶数,
即a+b和a-b的奇偶性相同;
(4)由(3)的结论:
-a+b=b-a与a+b=b+a奇偶性相同,
-a-b=-b-a与a-b=-b+a奇偶性相同,
因此-a+b、-a-b、a+b、a-b“同奇”或“同偶”;
(5)在2016个自然数1,2,3,…,2015,2016的每一个数的前面任意添加“+”或“-”,则其代数和一定是偶数.
故答案为:2n,2n+1或2n-1;是;偶数.
点评 本题主要考查了整式的加减,奇数与偶数的意义及推到偶数+偶数=偶数,奇数+奇数=偶数的过程.

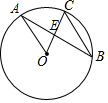 如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
| A. | a3+a3=2a6 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a2÷a5=a-3 |
 如图所示,在圆⊙O内有折线OAB,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )
如图所示,在圆⊙O内有折线OAB,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )| A. | 20 | B. | 19 | C. | 18 | D. | 16 |
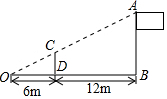 如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m.
如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m. 已知函数y=ax+b的大致图象如图所示,那么二次函数y=ax2+bx+1的图象可能是( )
已知函数y=ax+b的大致图象如图所示,那么二次函数y=ax2+bx+1的图象可能是( )


