题目内容
13.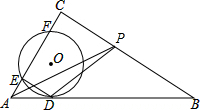 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长为4π,AF=CE,P是边BC上的动点,连结AP、DP,则AP+DP的最小值是24$\sqrt{7}$.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长为4π,AF=CE,P是边BC上的动点,连结AP、DP,则AP+DP的最小值是24$\sqrt{7}$.
分析 由弧DE的长度为4π,可以求得∠DOE的度数,再根据切线的性质可求得∠EDA的度数,即可证明DE∥BC,证得∠DEF=∠C=90°,得出FD是⊙0的直径,求得∠EFD=$\frac{1}{2}$∠EOD=30°,解直角三角形求得EF=12$\sqrt{3}$,进而求得AE=4$\sqrt{3}$,AD=8$\sqrt{3}$,进一步求得CA=20$\sqrt{3}$,AB=40$\sqrt{3}$,BC=60,根据三角形相似求得DK,即可求得DD′,解直角三角形求得DH、D′H,最后根据勾股定理求得AD′.
解答 解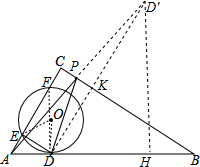 :连接OD、OE,
:连接OD、OE,
∵AD是⊙O的切线,
∴OD⊥AB,∴∠ODA=90°,
又∵弧DE的长度为4π,
∴4π=$\frac{nπ×12}{180}$,
∴n=60,
∴△ODE是等边三角形,
∴∠ODE=60°,
∴∠EDA=30°,
∴∠B=∠EDA,
∴DE∥BC.
∴∠DEF=∠C=90°,
∴FD是⊙0的直径,
∴∠EFD=$\frac{1}{2}$∠EOD=30°,
∵FD=24,
∴EF=12$\sqrt{3}$,
又∵∠EDA=30°,DE=OE=OD=12,
∴AE=4$\sqrt{3}$,
∴AD=8$\sqrt{3}$,
又∵AF=CE,
∴AE=CF,
∴CA=AE+EF+CF=20$\sqrt{3}$,
∴AB=40$\sqrt{3}$,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=60,
作D关于BC的对称点D′,DD′交BC于K,连接AD′,交BC于P,此时AP+DP的值最小,等于AD′,
∵∠DEF=∠C=90°,DD′⊥BC,
∴四边形EDKC是矩形,
∴DD′∥AC,
∴△DBK∽△ABC,
∴$\frac{BD}{AB}$=$\frac{DK}{AC}$,即$\frac{40\sqrt{3}-8\sqrt{3}}{40\sqrt{3}}$=$\frac{DK}{20\sqrt{3}}$,
∴DK=16$\sqrt{3}$,
∴DD′=32$\sqrt{3}$,
作D′H⊥AB于H,
∵∠KDB=∠BAC=60°,
∴DH=$\frac{1}{2}$DD′=16$\sqrt{3}$,D′H=$\frac{\sqrt{3}}{2}$DD′=48,
∴AH=8$\sqrt{3}$+16$\sqrt{3}$=24$\sqrt{3}$,
∴AD′=$\sqrt{A{H}^{2}+DH{′}^{2}}$=24$\sqrt{7}$.
故答案为24$\sqrt{7}$.
点评 本题考查了切线的性质,圆周角定理,勾股定理,轴对称-最短路线问题,解答本题的关键在于90°的圆周角对的弦是直径这一性质的灵活运用.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案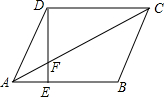 如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )
如图,在平行四边形ABCD中,AE:EB=1:2,如果S△AEF=4cm2,那么S△DCF=( )| A. | 12cm2 | B. | 24cm2 | C. | 36cm2 | D. | 48cm2 |
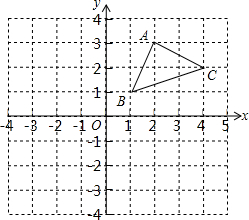 如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).
如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).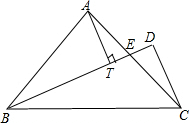 如图,等腰Rt△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC交AC于E,过C作CD⊥BE于D点,写出AT、CD与BD之间的数量关系并证明.
如图,等腰Rt△ABC中,∠BAC=90°,AB=AC,BE平分∠ABC交AC于E,过C作CD⊥BE于D点,写出AT、CD与BD之间的数量关系并证明.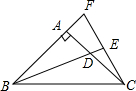 如图,把Rt△ABD绕点A逆时针旋转90°至△ACF的位置,BD的延长线交CF于点E,连接BC,若∠FBE=∠CBE,试确定CE与BD的关系.
如图,把Rt△ABD绕点A逆时针旋转90°至△ACF的位置,BD的延长线交CF于点E,连接BC,若∠FBE=∠CBE,试确定CE与BD的关系.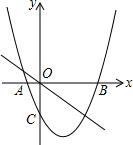 已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C.
已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C. 在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题: 如图是一个直角三角形,若以这个直角三角形的一边为边画一个等腰三角形,使它的第三个顶点在这个直角三角形的其他边上,那么这样的等腰三角形在图中能够作出的个数为6.
如图是一个直角三角形,若以这个直角三角形的一边为边画一个等腰三角形,使它的第三个顶点在这个直角三角形的其他边上,那么这样的等腰三角形在图中能够作出的个数为6.