题目内容
1.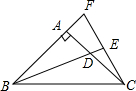 如图,把Rt△ABD绕点A逆时针旋转90°至△ACF的位置,BD的延长线交CF于点E,连接BC,若∠FBE=∠CBE,试确定CE与BD的关系.
如图,把Rt△ABD绕点A逆时针旋转90°至△ACF的位置,BD的延长线交CF于点E,连接BC,若∠FBE=∠CBE,试确定CE与BD的关系.
分析 由旋转的性质得出△ACF≌△ABD,得出CF=BD,∠ACF=∠ABD,由直角三角形的性质和对顶角相等得出∠ACF+∠CDE=90°,因此∠CED=90°,CE⊥BD,由ASA证明△BCE≌△BFE,得出对应边相等BC=BF,由等腰三角形的三线合一性质得出CE=FE=$\frac{1}{2}$CF,即可得出结论.
解答 解:CE⊥BD,CE=$\frac{1}{2}$BD;理由如下:
由旋转的性质得:△ACF≌△ABD,
∴CF=BD,∠ACF=∠ABD,
∵∠BAD=90°,
∴∠ABD+∠ADB=90°,
∵∠CDE=∠ADB,
∴∠ACF+∠CDE=90°,
∴∠CED=90°,
∴CE⊥BD,
即CE⊥BD,
在△BCE和△BFE中,$\left\{\begin{array}{l}{∠CBE=∠FBE}&{\;}\\{BE=BE}&{\;}\\{∠BEC=∠BEF=90°}&{\;}\end{array}\right.$,
∴△BCE≌△BFE(ASA),
∴BC=BF,
∴CE=FE=$\frac{1}{2}$CF,
∴CE=$\frac{1}{2}$BD.
点评 本题考查了全等三角形的判定与性质、旋转的性质、直角三角形的性质、等腰三角形的判定与性质;熟练掌握旋转的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
19.如果x=6是方程2x+3a=6x的解,那么a的值是( )
| A. | 4 | B. | 8 | C. | 9 | D. | -8 |
20.已知α为锐角,且$\sqrt{3}$tan(α+10°)=1,则α的度数为( )
| A. | 30° | B. | 45° | C. | 20° | D. | 35° |
 已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE.
已知△ABC中,AC=BC,∠ACB=90°,D,E分别为AB,BC上一点,连接DE.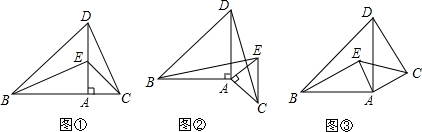
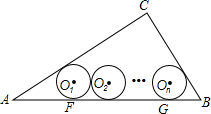 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,其中⊙O1,⊙O2,…⊙On,为n个(n≥2)相等的圆,⊙O1与⊙O2相外切,⊙O2与⊙O3相外切…,⊙On-1与⊙On相外切,⊙O1,⊙O2,…,⊙On都与AB相切,且⊙O1与AC相切,⊙On与BC相切,求这些等圆的半径r(用n表示).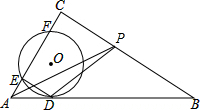 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长为4π,AF=CE,P是边BC上的动点,连结AP、DP,则AP+DP的最小值是24$\sqrt{7}$.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长为4π,AF=CE,P是边BC上的动点,连结AP、DP,则AP+DP的最小值是24$\sqrt{7}$. 如图,已知A,B,C,D四个点.
如图,已知A,B,C,D四个点.