题目内容
8.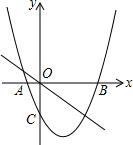 已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C.
已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C.(1)求A、B、C三点的坐标;
(2)若点P是抛物线上的动点,点Q是直线y=-x上的动点,若以点P,Q,C,O为顶点的四边形为平行四边形,求点P的坐标.
分析 (1)通过解方程x2-2x-3=0可确定A点和B点坐标;通过计算自变量为0时的函数值可确定C点坐标;
(2)根据二次函数图象上点的坐标特征,设P(t,t2-2t-3),则利用平行四边形的性质得到PQ=OC=3,PQ∥OC,于是可表示出Q点的坐标(t,-t),则|t2-2t-3+t|=3,然后去绝对符号得到两个关于t的一元二次方程,解方程求出t即可得到P点坐标.
解答 解:(1)当y=0时,x2-2x-3=0,解得x1=-1,x2=3,则A(-1,0),B(3,0);
当x=0时,y=x2-2x-3=-3,则C(0,-3);
(2)设P(t,t2-2t-3),如图,
∵四边形OCPQ为平行四边形,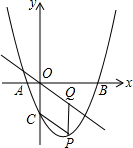
∴PQ=OC=3,PQ∥OC,
∴Q点的坐标可表示为(t,-t),
∴|t2-2t-3+t|=3,
当t2-2t-3+t=3,解得t1=3,t2=-2,
当t2-2t-3+t=-3,解得t1=0(舍去),t2=1,
综上所述,满足条件的P点坐标为(3,0)或(1,-4)或(-2,5).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了平行四边形的性质.

练习册系列答案
相关题目
20.如果$\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$是方程x+ay=$\frac{1}{2}$的解,则a的取值是( )
| A. | -1 | B. | -$\frac{1}{8}$ | C. | -3 | D. | -$\frac{3}{8}$ |
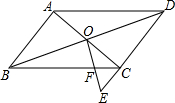 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,AB=2,BC=3,CE=1,则CF=$\frac{3}{4}$.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,AB=2,BC=3,CE=1,则CF=$\frac{3}{4}$.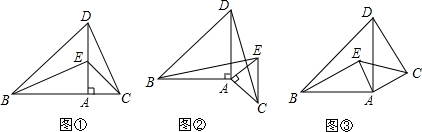
 如图:等边三角形ABC和CDE,
如图:等边三角形ABC和CDE,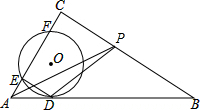 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长为4π,AF=CE,P是边BC上的动点,连结AP、DP,则AP+DP的最小值是24$\sqrt{7}$.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长为4π,AF=CE,P是边BC上的动点,连结AP、DP,则AP+DP的最小值是24$\sqrt{7}$.