题目内容
6.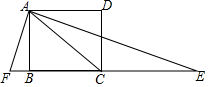 如图,矩形ABCD中,BC=4,AB=3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为( )
如图,矩形ABCD中,BC=4,AB=3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为( )| A. | 8 | B. | 9 | C. | 10 | D. | $\frac{81}{8}$ |
分析 利用矩形的性质和勾股定理可得AC的长,由角平分线的性质和平行线的性质可得∠CAE=∠E,易得CE=CA,由FA⊥AE,可得∠FAC=∠F,易得CF=AC,可得EF的长.
解答 解:
∵四边形ABCD为矩形,且AB=3,BC=4,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵AE平分∠CAD,
∴∠CAE=∠DAE,
∵AD∥CE,
∴∠DAE=∠E,
∴∠CAE=∠E,
∴CE=CA=5,
∵FA⊥AE,
∴∠FAC+∠CAE=90°,∠F+∠E=90°,
∴∠FAC=∠F,
∴CF=AC=5,
∴EF=CF+CE=10,
故选C.
点评 本题主要考查了矩形的性质和等腰三角形的判定,求得CF=AC是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
16.下列运算正确的是( )
| A. | a3-a3=a0 | B. | a2÷a-1=a3 | C. | a2+a2=2a4 | D. | a3×a3=a3 |
17.如图,下列各图象反映的是两个变量之间的关系,其中表示匀速运动的是( )


| A. | (3)(4) | B. | (2)(3) | C. | (1)(2) | D. | (2)(4) |
14.直线y=2x经过( )
| A. | 第二、四象限 | B. | 第一、二象限 | C. | 第三、四象限 | D. | 第一、三象限 |
1.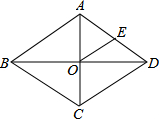 如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )
如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )
 如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )
如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )| A. | 3.5 | B. | 4 | C. | 7 | D. | 14 |
11. 实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{{a}^{2}}$的结果为( )
实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{{a}^{2}}$的结果为( )
 实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{{a}^{2}}$的结果为( )
实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{{a}^{2}}$的结果为( )| A. | b | B. | 2a-b | C. | -b | D. | b-2a |
18.在数学竞赛的选拔活动中,对甲、乙两名同学的成绩经过统计分析可得:$\overline{{x}_{甲}}$=94(分),$\overline{{x}_{乙}}$=94(分);S${\;}_{甲}^{2}$=1.02,S${\;}_{乙}^{2}$=0.85,下列结论正确的是( )
| A. | 甲的成绩比乙的成绩好 | B. | 甲的成绩比乙的成绩稳定 | ||
| C. | 应该选择乙同学参加竞赛 | D. | 不能衡量两名同学的成绩优劣 |
15. 如图所示,?ABCD的对角线AC,BD相交于点O,点E是CD的中点,若BC=6,则OE的长为( )
如图所示,?ABCD的对角线AC,BD相交于点O,点E是CD的中点,若BC=6,则OE的长为( )
 如图所示,?ABCD的对角线AC,BD相交于点O,点E是CD的中点,若BC=6,则OE的长为( )
如图所示,?ABCD的对角线AC,BD相交于点O,点E是CD的中点,若BC=6,则OE的长为( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 4 |
16.下列命题中,原命题是假命题,而逆命题是真命题的是( )
| A. | 两个全等三角形的面积相等 | |
| B. | 两条高线相等的三角形是等腰三角形 | |
| C. | 相等的角是对顶角 | |
| D. | 线段的垂直平分线上的点到线段两端点距离相等 |