题目内容
1.求不等式组$\left\{\begin{array}{l}{2(x+1)>3x-1}\\{\frac{x+2}{3}≥1}\end{array}\right.$的正整数解.分析 先求出每个不等式的解集,再求出不等式组的解集,即可得出答案.
解答 解:$\left\{\begin{array}{l}{2(x+1)>3x-1①}\\{\frac{x+2}{3}≥1②}\end{array}\right.$
∵解不等式①得:x<3,
解不等式②得:x≥1,
∴不等式组的解集为1≤x<3,
∴不等式组的正整数解为1,2.
点评 本题考查了解一元一次不等式组,不等式组的整数解的应用,能求出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
16.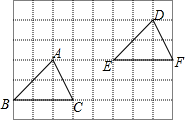 如图,△ABC经过怎样的平移得到△DEF( )
如图,△ABC经过怎样的平移得到△DEF( )
 如图,△ABC经过怎样的平移得到△DEF( )
如图,△ABC经过怎样的平移得到△DEF( )| A. | 把△ABC向左平移5个单位,再向下平移2个单位 | |
| B. | 把△ABC向右平移5个单位,再向下平移2个单位 | |
| C. | 把△ABC向右平移5个单位,再向上平移2个单位 | |
| D. | 把△ABC向左平移5个单位,再向上平移两个单位 |
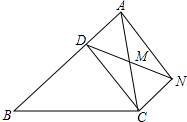 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.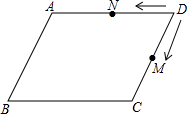 如图,?ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,两点均运动到点D停止.
如图,?ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,两点均运动到点D停止.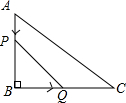 如图,在△ABC中,∠B=90°,tan∠C=$\frac{3}{4}$,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
如图,在△ABC中,∠B=90°,tan∠C=$\frac{3}{4}$,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )