题目内容
11.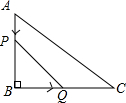 如图,在△ABC中,∠B=90°,tan∠C=$\frac{3}{4}$,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
如图,在△ABC中,∠B=90°,tan∠C=$\frac{3}{4}$,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )| A. | 18cm2 | B. | 12cm2 | C. | 9cm2 | D. | 3cm2 |
分析 先根据已知求边长BC,再根据点P和Q的速度表示BP和BQ的长,设△PBQ的面积为S,利用直角三角形的面积公式列关于S与t的函数关系式,并求最值即可.
解答 解:∵tan∠C=$\frac{3}{4}$,AB=6cm,
∴$\frac{AB}{BC}=\frac{6}{BC}$=$\frac{3}{4}$,
∴BC=8,
由题意得:AP=t,BP=6-t,BQ=2t,
设△PBQ的面积为S,
则S=$\frac{1}{2}$×BP×BQ=$\frac{1}{2}$×2t×(6-t),
S=-t2+6t=-(t2-6t+9-9)=-(t-3)2+9,
P:0≤t≤6,Q:0≤t≤4,
∴当t=3时,S有最大值为9,
即当t=3时,△PBQ的最大面积为9cm2;
故选C.
点评 本题考查了有关于直角三角形的动点型问题,考查了解直角三角形的有关知识和二次函数的最值问题,解决此类问题的关键是正确表示两动点的路程(路程=时间×速度);这类动点型问题一般情况都是求三角形面积或四边形面积的最值问题,转化为函数求最值问题,直接利用面积公式或求和、求差表示面积的方法求出函数的解析式,再根据函数图象确定最值,要注意时间的取值范围.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
2. 如图,是一次函数y=ax+b的图象,那么a、b的取值范围是( )
如图,是一次函数y=ax+b的图象,那么a、b的取值范围是( )
 如图,是一次函数y=ax+b的图象,那么a、b的取值范围是( )
如图,是一次函数y=ax+b的图象,那么a、b的取值范围是( )| A. | a>0,b>0 | B. | a<0,b>0 | C. | a>1,b>0 | D. | a<1,b>0 |
19.下列图形中是中心对称图形,但不一定是轴对称的是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 平行四边形 |
 在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过6秒该直线可将平行四边形OABC的面积平分.
在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过6秒该直线可将平行四边形OABC的面积平分.



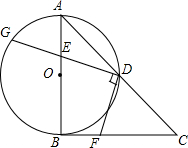 如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.