题目内容
3. 如图,在?ABCD中,∠ABC的平分线BM交CD于点M,且MC=2,?ABCD的周长是14,则DM等于3.
如图,在?ABCD中,∠ABC的平分线BM交CD于点M,且MC=2,?ABCD的周长是14,则DM等于3.
分析 根据BM是∠ABC的平分线和AB∥CD,求出BC=MC=2,根据?ABCD的周长是14,求出CD=5,即可得到DM的长.
解答 解:∵BM是∠ABC的平分线,
∴∠ABM=∠CBM,
∵AB∥CD,
∴∠ABM=∠BMC,
∴∠BMC=∠CBM,
∴BC=MC=2,
∵?ABCD的周长是14,
∴BC+CD=7,
∴CD=5,
则DM=CD-MC=3,
故答案为:3.
点评 本题考查了平行四边形的性质和角平分线的定义,根据平行四边形的对边相等求出BC+CD是解题的关键,注意等腰三角形的性质的正确运用.

练习册系列答案
相关题目
13.下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③$\frac{x}{2}+\frac{x}{3}$=4去分母的3x+2x=24;
④(x+2)-2(x-1)=0去括号得x+2-2x-2=0.
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③$\frac{x}{2}+\frac{x}{3}$=4去分母的3x+2x=24;
④(x+2)-2(x-1)=0去括号得x+2-2x-2=0.
| A. | ①③ | B. | ①②③ | C. | ①④ | D. | ①③④ |
14. 平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
 平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )| A. | 61° | B. | 63° | C. | 65° | D. | 67° |
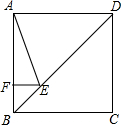 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于点F,求EF的长.
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于点F,求EF的长. 如图,在正方形ABCD中,以CD为边向外作等边三角形CDE,连结AE、BE,则∠AEB=30°.
如图,在正方形ABCD中,以CD为边向外作等边三角形CDE,连结AE、BE,则∠AEB=30°. 如图,在平面直角坐标系中,菱形OBCD的顶点O、D的坐标分别是(0、0)、(3、4),求顶点C的坐标.
如图,在平面直角坐标系中,菱形OBCD的顶点O、D的坐标分别是(0、0)、(3、4),求顶点C的坐标.