题目内容
11.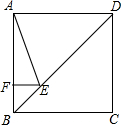 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于点F,求EF的长.
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于点F,求EF的长.
分析 首先由正方形ABCD中,∠BAE=22.5°,证得DA=DE,继而求得BE=BD-DE,然后由等腰直角三角形的性质,求得答案.
解答 解∵四边形ABCD是正方形,
∴∠BAD=90°,∠ABD=∠ADB=45°.
∵∠BAE=22.5°,
∴∠DAE=67.5°,
∴∠DEA=67.5°.
∴DA=DE,
∵正方形的边长为4,
∴DE=AD=4,BD=4$\sqrt{2}$.
∴BE=4$\sqrt{2}$-4.
∴EF=$\frac{\sqrt{2}}{2}$BE=$\frac{\sqrt{2}}{2}$(4$\sqrt{2}$-4)=4-2$\sqrt{2}$.
点评 此题考查了正方形的性质、等腰三角形的判定与性质以及等腰直角三角形的性质.注意证得△ADE是等腰三角形是解此题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.如果反比例函数y=$\frac{k}{x}$的图象经过点(3,-2),则k的值是( )
| A. | -6 | B. | 6 | C. | -3 | D. | 3 |
16.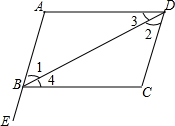 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠C=∠CBE | D. | ∠C+∠ABC=180° |
20.下列图案既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
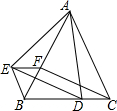 如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF. 如图,在?ABCD中,∠ABC的平分线BM交CD于点M,且MC=2,?ABCD的周长是14,则DM等于3.
如图,在?ABCD中,∠ABC的平分线BM交CD于点M,且MC=2,?ABCD的周长是14,则DM等于3.