题目内容
14．
平行四边形ABCD中，对角线AC与BD交于点O，∠DAC=42°，∠CBD=23°，则∠COD是（ ）| A． | 61° | B． | 63° | C． | 65° | D． | 67° |
分析 由平行四边形的性质得出∠BCA=∠DAC=42°，再由三角形的外角性质得出∠COD=∠CBD+∠BCA，即可得出结果．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠BCA=∠DAC=42°，
∴∠COD=∠CBD+∠BCA=42°+23°=65°．
故答案为：65°．
点评 本题考查了平行四边形的性质、三角形的外角性质；熟练掌握平行四边形的性质，由三角形的外角性质得出∠COD=∠CBD+∠BCA是解决问题的关键．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
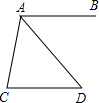如图，AB∥CD，AD平分∠BAC，且∠C=80°，则∠D的度数为50°．
如图所示，AO⊥BO，CO⊥DO，∠AOC：∠BOC=1：4，则∠BOD=150°．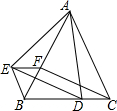
如图，△ABC和△BEF都是等边三角形，点D在BC边上，点F在AB边上，且∠EAD=60°，连接ED、CF．
如图，在?ABCD中，∠ABC的平分线BM交CD于点M，且MC=2，?ABCD的周长是14，则DM等于3．
4．$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$，是二元一次方程2x+ay=3的一个解，则a的值为（ ）
| A． | 3 | B． | $\frac{1}{3}$ | C． | 1 | D． | -1 |