题目内容
9. 如图,AB=AC,∠BAC=90°,以AB为直径作⊙O,OC交⊙O于D,延长BD交AC于E,求$\frac{CE}{AE}$的值.
如图,AB=AC,∠BAC=90°,以AB为直径作⊙O,OC交⊙O于D,延长BD交AC于E,求$\frac{CE}{AE}$的值.
分析 连接AD,设⊙O的半径为r,由圆周角定理和已知条件得出∠B=∠DAC,由勾股定理求出OC,由等腰三角形的性质和对顶角相等得出∠CDE=∠DAC,周长△CDE∽△ACD,得出对应边成比例$\frac{CD}{AC}=\frac{CE}{CD}$,求出CE,得出AE.
解答 解:连接AD,如图所示: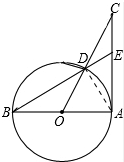 设⊙O的半径为r,
设⊙O的半径为r,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠B=∠DAC,OC=$\sqrt{O{A}^{2}+A{C}^{2}}$=$\sqrt{5}$r,
∵OB=OD,
∴∠B=∠ODB=∠CDE,
∴∠CDE=∠DAC,
又∵∠C=∠C,
∴△CDE∽△ACD,
∴$\frac{CD}{AC}=\frac{CE}{CD}$,
即$\frac{(\sqrt{5}-1)r}{2r}=\frac{CE}{(\sqrt{5}-1)r}$,
∴CE=(3-$\sqrt{5}$)r,
∴AE=AC-CE=($\sqrt{5}$-1)r,
∴$\frac{CE}{AE}$=$\frac{3-\sqrt{5}}{\sqrt{5}-1}$=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了相似三角形的判定与性质、圆周角定理、等腰三角形的性质;熟练掌握圆周角定理,证明三角形相似是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知,点A(-2,y1),B(-1,y2),C(1,y3)都在函数y=-2x+b的图象上,则关于y1,y2,y3的大小关系正确的是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y3<y1<y2 |
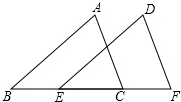 如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.
如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.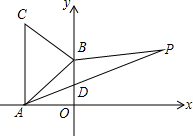 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内. 如图,DE,FG分别是AB,AC的中垂线,若AB=8,AC=5,BC=11,则△ADF的周长=11.
如图,DE,FG分别是AB,AC的中垂线,若AB=8,AC=5,BC=11,则△ADF的周长=11.