题目内容
10.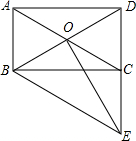 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E,连接OE.
如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E,连接OE.(1)求证:BD=BE;
(2)若BO=AB,试判断线段OE、OD的数量关系,并说明理由.
分析 (1)根据矩形的对角线相等可得AC=BD,对边平行可得AB∥CD,再求出四边形ABEC是平行四边形,根据平行四边形的对边相等可得AC=BE,从而得证.
(2)由矩形的性质和已知条件证出△AOB是等边三角形,得出∠ABO=60°,再证明△BDE是等边三角形,然后运用等边三角形的性质和三角函数即可得出结论.
解答 (1)证明:∵四边形ABCD是矩形,
∴AC=BD,AB∥CD,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
(2)解:OE=$\sqrt{3}$OD;理由如下:
∵四边形ABCD是矩形,
∴AC=BD,AB∥CD,BO=DO=$\frac{1}{2}$BD,OA=OC=$\frac{1}{2}$AC,
∴OA=BO,
∵BO=AB,
∴BO=AB=OA,即△AOB是等边三角形,
∴∠ABO=60°,
∵AB∥CD,
∴∠BDE=∠ABO=60°,
由(1)得:BD=BE,
∴△BDE是等边三角形,
又∵BO=DO,
∴OE⊥BD,
∴OE=$\sqrt{3}$OD.
点评 本题考查了矩形的性质,平行四边形的判定与性质、等边三角形的判定与性质;熟练掌握矩形的性质,证明△BDE是等边三角形是解决问题(2)的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
18.已知,点A(-2,y1),B(-1,y2),C(1,y3)都在函数y=-2x+b的图象上,则关于y1,y2,y3的大小关系正确的是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y3<y1<y2 |
20.已知(a+3)2+|b-2|+2=b,则a、b的值是( )
| A. | a=-3,b为任意值 | B. | a=3,b为任意值 | C. | a=-3,b≥2 | D. | 不存在这样的a、b |
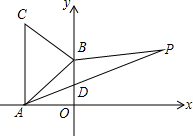 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.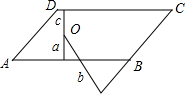 如图,在平行四边形ABCD中,AB=2AD,点O为平行四边形内一点,它到直线AB,BC,CD距离分别为a,b,c,且它到AD和CD的距离相等,则2a-b+c=0.
如图,在平行四边形ABCD中,AB=2AD,点O为平行四边形内一点,它到直线AB,BC,CD距离分别为a,b,c,且它到AD和CD的距离相等,则2a-b+c=0.