题目内容
7.若ax=3,则a3x=27;若3m=5,3n=2,则3m+2n=20.分析 利用幂的乘方运算法则结合同底数幂的乘法运算法则将原式变形求出答案.
解答 解:∵ax=3,
∴a3x=(ax)3=33=27;
∵3m=5,3n=2,
∴3m+2n=3m×(3n)2=5×22=20.
故答案为:27,20.
点评 此题主要考查了幂的乘方运算以及同底数幂的乘法运算,正确化简各式是解题关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
18.下列五种图形中,正方体的截平面不可能出现的图形有( )
(1)钝角三角形;(2)直角三角形;(3)菱形;(4)正五边形;(5)正六边形.
(1)钝角三角形;(2)直角三角形;(3)菱形;(4)正五边形;(5)正六边形.
| A. | (1)(2)(5) | B. | (1)(2)(4) | C. | (2)(3)(4) | D. | (3)(4)(5) |
15.若(m-2)x|m|+2x-1=0是关于x的一元二次方程,则m的值为( )
| A. | m=±2 | B. | m=2 | C. | m=-2 | D. | 无法确定 |
12.以下问题,不适合用全面调查的是( )
| A. | 了解全班同学每周零花钱的情况 | B. | 旅客上飞机前的安检 | ||
| C. | 工厂招聘工人,对应聘人员体检 | D. | 了解全国中小学生的身高情况 |
17.已知点A(2a+1,5a-2)在第一、三象限的角平分线上,点B(2m+7,m-1)在二、四象限的角平分线上,则( )
| A. | a=1,m=-2 | B. | a=1,m=2 | C. | a=-1,m=-2 | D. | a=-1,m=2 |
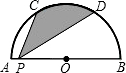 如图,C、D是直径为4的半圆O上的三等分点,P是直径AB上的任意一点,连接CP、DP,则图中阴影部分的面积是$\frac{2}{3}$π.
如图,C、D是直径为4的半圆O上的三等分点,P是直径AB上的任意一点,连接CP、DP,则图中阴影部分的面积是$\frac{2}{3}$π.
 如图所示,已知∠AOB=90°,∠BOC=40°,OD平分∠AOC,求∠BOD的度数.
如图所示,已知∠AOB=90°,∠BOC=40°,OD平分∠AOC,求∠BOD的度数.