题目内容
7.如图,在平面直角坐标系xOy中.抛物线y=mx2-2mx-3m(m<0)与x轴交于A、B两点(点A在点B的左侧).(1)点A的坐标为(-1,0)抛物线的对称轴为x=1
(2)经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D.且AD=5AC.
①求直线l的函数表达式(其中k、b用含m的式子表示);
②设P是抛物线的对称轴上的一点.点Q在抛物线上.以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点p的坐标,若不能,请说明理由.

分析 (1)设y=0即可求出的A坐标,根据对称轴x=-$\frac{b}{2a}$可以求出对称轴.
(2)①如图1,作DF⊥x轴于F,由DF∥OC得$\frac{OF}{OA}=\frac{CD}{AC}$=4,可以求出点D坐标,由A、D坐标可以求出直线AD.
②分两种情形讨论即:Ⅰ若AD是矩形的一条边,利用勾股定理列出方程解决;Ⅱ如图3中,若AD是矩形的一条对角线,列出方程即可解决问题.
解答 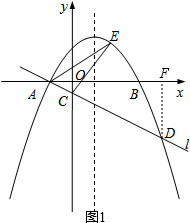 解:(1)令y=0,则mx2-2mx-3m=0,
解:(1)令y=0,则mx2-2mx-3m=0,
解得x1=-1,x2=3
∵点A在点B的左侧,
∴A(-1,0),对称轴x=-$\frac{-2m}{2m}$=1,
故答案分别为A(-1,0),x=1.
(2)①如图1,作DF⊥x轴于F,
∴DF∥OC,
∴$\frac{OF}{OA}=\frac{CD}{AC}$,
∵AD=5AC,
∴$\frac{OF}{OA}$=$\frac{DC}{AC}$=4,
∵OA=1,
∴OF=4,
∴D点的横坐标为4,
代入y=mx2-2mx-3m得,y=5m,
∴D(4,5m),
把A、D坐标代入y=kx+b得到$\left\{\begin{array}{l}{-k+b=0}\\{4k+b=5m}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=m}\\{b=m}\end{array}\right.$,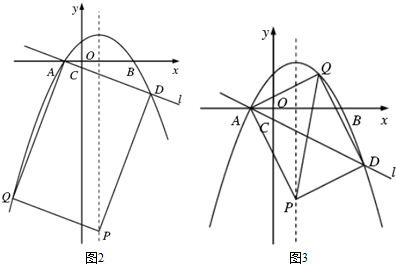
∴直线l的函数表达式为y=mx+m.
②Ⅰ若AD是矩形的一条边,
由AQ∥DP知xD-xP=xA-xQ,可知Q点横坐标为-4,将x=-4代入抛物线方程得Q(-4,21m),
yP=yD+yQ=5m+21m=26m,则P(1,26m),
∵四边形ADPQ为矩形,∴∠ADP=90°,
∴AD2+PD2=AP2,
∵AD2=[4-(-1)]2+(5m)2=52+(5m)2,
PD2=[1-4]2+(26m-5m)2=32+(21m)2,
PA2=(1+1)2+(26m)2
∴52+(5m)2+32+(21m)2=22+(26m)2
∴m2=$\frac{1}{7}$,∵m<0,∴m=-$\frac{\sqrt{7}}{7}$,
∴P(1,-$\frac{26\sqrt{7}}{7}$).
Ⅱ如图3中,若AD是矩形的一条对角线,则线段AD的中点坐标为($\frac{3}{2}$,2.5m),点P的横坐标为1,则Q(2,-3m),由AQ2+QD2=AD2,得到32+(3m)2+22+(8m)2=52+(5m)2,
解得m2=$\frac{1}{4}$,∵m<0,
∴m=-$\frac{1}{2}$,
∴点P坐标(1,-4)
综上所述点P(1,-$\frac{26\sqrt{7}}{7}$)或(1,-4).
点评 本题考查二次函数的有关知识,一次函数的有关知识,矩形的性质,解题的关键是灵活应用待定系数法确定函数解析式,学会分类讨论的思想,把问题转化为方程解决,属于中考压轴题.

(1)a1,3=10;
(2)表中这九个数的中位数是4;
(3)如果从表中这九个数中随机抽取一个数,那么抽到可能性最大的数是3;
(4)如果从表中这九个数中随机抽取一个数,那么抽到素数的概率是$\frac{2}{3}$.
| a1,1 | a1,2 | a1,3 |
| a2,1 | a2,2 | a2,3 |
| a3,1 | a3,2 | a3,3 |
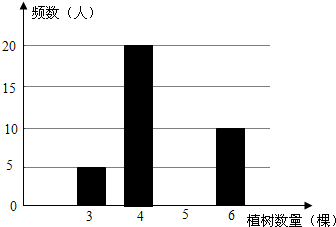 学校组织师生开展植树造林活动,为了了解全校4000名学生的情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
学校组织师生开展植树造林活动,为了了解全校4000名学生的情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的平均数;
(3)根据抽样数据,估计该校4000名学生的植树数量.
| 植树数量 (棵) | 频数 (人) | 频率 |
| 3 | 5 | 0.1 |
| 4 | 20 | 0.4 |
| 5 | 15 | 0.3 |
| 6 | 10 | 0.2 |
| 合计 | 50 | 1 |
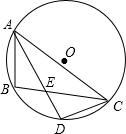 如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.
如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.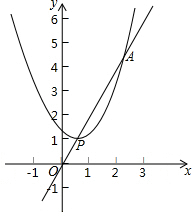 如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.
如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.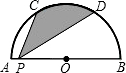 如图,C、D是直径为4的半圆O上的三等分点,P是直径AB上的任意一点,连接CP、DP,则图中阴影部分的面积是$\frac{2}{3}$π.
如图,C、D是直径为4的半圆O上的三等分点,P是直径AB上的任意一点,连接CP、DP,则图中阴影部分的面积是$\frac{2}{3}$π.