题目内容
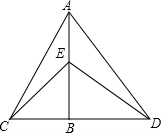 如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,下列说法中:①△ABC≌△DBE;②△ACB≌△ABD;③△CBE≌△BED;④△ACE≌△ADE.正确的是( )
如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,下列说法中:①△ABC≌△DBE;②△ACB≌△ABD;③△CBE≌△BED;④△ACE≌△ADE.正确的是( )| A、①②③ | B、① |
| C、①③④ | D、②③④ |
考点:全等三角形的判定,等腰直角三角形
专题:
分析:根据△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,利用全等三角形的判定定理对4个结论逐个分析即可.
解答:解:①△ABC≌△DBE,BC=BE,∠ABC=∠DBE=90°,AB=BD,符合SAS,故①正确;
②△ACB与△ABD不全等,因为它们的形状不相同,
△ACB只是直角三角形,△ABD是等腰直角三角形,故②错误;
③△CBE与△BED不全等,理由同②,故③错误;
④△ACE与△ADE不全等,它们只有一边一角对应相等,故④错误;
故选B.
②△ACB与△ABD不全等,因为它们的形状不相同,
△ACB只是直角三角形,△ABD是等腰直角三角形,故②错误;
③△CBE与△BED不全等,理由同②,故③错误;
④△ACE与△ADE不全等,它们只有一边一角对应相等,故④错误;
故选B.
点评:本题考查了全等三角形的判定,以及还考查了学生对等腰直角三角形和全等三角形的判定的理解和掌握,此题难度不大,根据全等三角形的判定定理即可判断出.

练习册系列答案
相关题目
2015年1月1日,《深圳经济特区促进全民健条例》正式实施,小颖为了了解她所在小区(约有3000人)市民的运动健身情况,她应采用的收集数据的方式是( )
| A、对小区所有成年人发放问卷进行调查 |
| B、对小区内所有中小学生发放问卷进行调查 |
| C、在小区出入口对出入居民随机发放问卷进行调查 |
| D、挨家挨户发放问卷进行调查 |
 如图,一艘渔船正由西向东追赶鱼群,在A处测得小岛C在船的北偏东60°方向,距离A处80千米,此时渔船接到通知,以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向前追赶鱼群,是否有进入区域的可能?
如图,一艘渔船正由西向东追赶鱼群,在A处测得小岛C在船的北偏东60°方向,距离A处80千米,此时渔船接到通知,以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向前追赶鱼群,是否有进入区域的可能? 如图,六边形ABCDEF的内角都相等,∠1=60°.
如图,六边形ABCDEF的内角都相等,∠1=60°.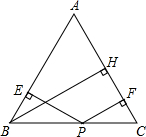 如图,已知等边三角形ABC中,P为底边BC上任意一点,PE⊥AB于E,PF⊥AC于F,BH⊥AC于H,求证:PE+PF=BH.
如图,已知等边三角形ABC中,P为底边BC上任意一点,PE⊥AB于E,PF⊥AC于F,BH⊥AC于H,求证:PE+PF=BH. 如图,直线AB、CD交EF于点G、H,∠2=∠3,∠1=70°,求∠4的度数.
如图,直线AB、CD交EF于点G、H,∠2=∠3,∠1=70°,求∠4的度数.