题目内容
已知,△ABC中,sinA=
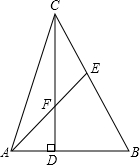
,点D为AB中点,点E、F分别是射线AC、CB上的点,连接DE、EF、DF,∠EDF=90°,∠A=∠EFD.
(1)求证:∠ACB=90°;
(2)若点D关于EF的对称点为N,连接CN,过点F作FH⊥CN交直线CN于点H,试探究CE、CN、FH三者之间的关系.并证明你的结论.

| 4 |
| 5 |
(1)求证:∠ACB=90°;
(2)若点D关于EF的对称点为N,连接CN,过点F作FH⊥CN交直线CN于点H,试探究CE、CN、FH三者之间的关系.并证明你的结论.

考点:相似形综合题
专题:
分析:(1)过点D作DH⊥AB交AC于点H,利用sinA=
,找出边角关系,证得△EHD∽△DFB,进一步得出结论即可;
(2)分两种情况探讨:当点E在AC上时,点E在AC延长线上时;利用相似三角形的判定与性质和锐角三角函数探讨得出答案即可.
| 4 |
| 5 |
(2)分两种情况探讨:当点E在AC上时,点E在AC延长线上时;利用相似三角形的判定与性质和锐角三角函数探讨得出答案即可.
解答:证明:过点D作DH⊥AB交AC于点H,

∵sinA=
,
∴在Rt△AHD中,
=
.
∵∠A=∠EFD,
∴在Rt△EFD中,
=
,
∴
=
∵AD=BD,
∴
=
.
∵∠EDF=∠ADH=90°,
∴∠EDH=∠FDB.
∴△EHD∽△DFB,
∴∠H=∠B,
∵∠CMH=∠DMF,
∴∠ACB=∠HDB=90°.
(2)当点E在AC上时,
过点N作NQ⊥BC于点Q,NP⊥AC于点P,
∴∠NPE=∠NQF=90°,
∵∠PNQ=∠ENF=90°
∴∠PNE=∠QNF,
∴△PNE∽△QNF
=
=
.
∵矩形PNQC,
∴PN=CQ
∴
=
,tan∠NCQ=tan∠B
∴∠NCQ=∠B
∴CH∥AB.
过点E作EM⊥CN于点M
∴∠MCE=∠A
∴
=
∴∠EMH=∠H=∠ENF=90°
∴△MNE∽△HFN
=
=
∴MN=
HF
∴
CE+CN=
HF.
第二情况当点E在AC延长线上时
同理可证CN-
CE=
HF.


∵sinA=
| 4 |
| 5 |
∴在Rt△AHD中,
| DH |
| AD |
| 4 |
| 3 |
∵∠A=∠EFD,
∴在Rt△EFD中,
| DE |
| DF |
| 4 |
| 3 |
∴
| DH |
| AD |
| DE |
| DF |
∵AD=BD,
∴
| DH |
| BD |
| DE |
| DF |
∵∠EDF=∠ADH=90°,
∴∠EDH=∠FDB.
∴△EHD∽△DFB,
∴∠H=∠B,
∵∠CMH=∠DMF,
∴∠ACB=∠HDB=90°.
(2)当点E在AC上时,
过点N作NQ⊥BC于点Q,NP⊥AC于点P,
∴∠NPE=∠NQF=90°,
∵∠PNQ=∠ENF=90°
∴∠PNE=∠QNF,
∴△PNE∽△QNF
| QN |
| PN |
| NF |
| NE |
| 3 |
| 4 |
∵矩形PNQC,
∴PN=CQ
∴
| QN |
| CQ |
| 3 |
| 4 |
∴∠NCQ=∠B
∴CH∥AB.
过点E作EM⊥CN于点M
∴∠MCE=∠A
∴
| MC |
| CE |
| 3 |
| 5 |
∴∠EMH=∠H=∠ENF=90°
∴△MNE∽△HFN
| HF |
| MN |
| NF |
| NE |
| 3 |
| 4 |
∴MN=
| 4 |
| 3 |
∴
| 3 |
| 5 |
| 4 |
| 3 |
第二情况当点E在AC延长线上时
同理可证CN-
| 3 |
| 5 |
| 4 |
| 3 |

点评:此题综合考查相似三角形的性质,锐角三角函数的运用,以及分类讨论思想的渗透,关键结合题目作出适当的辅助线是解决问题的关键.

练习册系列答案
相关题目
分式方程
=
的解是( )
| 4 |
| x+1 |
| 3 |
| x |
| A、x=1 | B、x=-1 |
| C、x=3 | D、x=-3 |
 已知:如图,在△ABC中,CD⊥AB于点D,AD=2,BD=3,CD=6,点E是BC上一点,
已知:如图,在△ABC中,CD⊥AB于点D,AD=2,BD=3,CD=6,点E是BC上一点,