题目内容
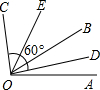 如图,∠AOB:∠BOC=3:5,又OD、OE分别是∠AOB和∠BOC的平分线,若∠DOC=60°,求∠AOB和∠BOC的度数.
如图,∠AOB:∠BOC=3:5,又OD、OE分别是∠AOB和∠BOC的平分线,若∠DOC=60°,求∠AOB和∠BOC的度数.考点:角的计算,角平分线的定义
专题:
分析:由∠AOB:∠BOC=3:5,可设∠AOB=3x,∠BOC=5x,由OD、OE分别是∠AOB和∠BOC的平分线,可得∠AOD=∠BOD=
∠AOB=1.5x,∠BOE=∠COE=
∠BOC=2.5x,由∠DOC=60°,∠DOC=∠DOB+∠BOE+∠COE,可以求出x的值,从而可求出∠AOB和∠BOC的度数.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠AOB:∠BOC=3:5,
∴设∠AOB=3x,则∠BOC=5x,
∵OD、OE分别是∠AOB和∠BOC的平分线,
∴∠AOD=∠BOD=
∠AOB=1.5x,∠BOE=∠COE=
∠BOC=2.5x,
∵∠DOC=∠DOB+∠BOE+∠COE,∠DOC=60°,
∴1.5x+2.5x+2.5x=60°,
∴x=
.
∴∠AOB=3x=(
)°,∠BOC=5x=(
)°.
∴设∠AOB=3x,则∠BOC=5x,
∵OD、OE分别是∠AOB和∠BOC的平分线,
∴∠AOD=∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DOC=∠DOB+∠BOE+∠COE,∠DOC=60°,
∴1.5x+2.5x+2.5x=60°,
∴x=
| 120 |
| 13 |
∴∠AOB=3x=(
| 360 |
| 13 |
| 600 |
| 13 |
点评:此题考查了角的计算,解题关键是由∠AOB:∠BOC=3:5,可设∠AOB=3x,∠BOC=5x,然后列方程解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,等边△ABC中,D是三角形内一点,DA=DB,BE=AB,∠CBD=∠EBD,求∠E的度数.
如图所示,等边△ABC中,D是三角形内一点,DA=DB,BE=AB,∠CBD=∠EBD,求∠E的度数. 已知点A在⊙O上,根据sinB=
已知点A在⊙O上,根据sinB=