题目内容
利用平方根去根号可以用一个无理数构造一个整系数方程,例如:a=
+1时,移项得a-1=
,两边平方得(a-1)2=(
)2.∴a2-2a+1=2,即a2-2a-1=0,仿照上述方法完成下面的题目.已知a=
,求:
(1)a2+a的值;
(2)a3-2a+2014的值.
| 2 |
| 2 |
| 2 |
| ||
| 2 |
(1)a2+a的值;
(2)a3-2a+2014的值.
考点:因式分解的应用,实数的运算
专题:阅读型
分析:(1)将a=
变形,得到2a+1=
,两边平方、化简即可解决问题.
(2)将所给的代数式变形、化简,借助(1)中的结论,代入计算,问题即可解决.
| ||
| 2 |
| 5 |
(2)将所给的代数式变形、化简,借助(1)中的结论,代入计算,问题即可解决.
解答:解:(1)∵a=
,
∴2a+1=
,
∴4a2+4a+1=5,
∴a2+a=1.
(2)∵a3-2a+2014
=a3-a-a+2014
=a(a2-1)-a+2014.
∵a2+a=1,
∴a2-1=-a,
∴a3-2a+2014
=-a2-a+2014
=2013.
| ||
| 2 |
∴2a+1=
| 5 |
∴4a2+4a+1=5,
∴a2+a=1.
(2)∵a3-2a+2014
=a3-a-a+2014
=a(a2-1)-a+2014.
∵a2+a=1,
∴a2-1=-a,
∴a3-2a+2014
=-a2-a+2014
=2013.
点评:该题主要考查了因式分解及其应用问题;解题的关键是灵活变形、正确化简运算、准确求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
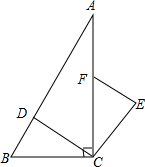 如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后的CE,连接EF.当CD⊥AB时,判断EF与CD的位置关系,并说明理由.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后的CE,连接EF.当CD⊥AB时,判断EF与CD的位置关系,并说明理由. 如图,10条20cm长的线段首尾黏合成一个纸圈,黏合部分的长度为1.5cm,则纸圈的周长为
如图,10条20cm长的线段首尾黏合成一个纸圈,黏合部分的长度为1.5cm,则纸圈的周长为