题目内容
12.点A(-1,-2),点B(3,4),则线段AB与x轴正半轴夹角的正弦值为( )| A. | $\frac{4}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{13}}{13}$ | D. | $\frac{2\sqrt{13}}{13}$ |
分析 如图,过A作AC∥x轴,过B作BC∥y轴,则∠C=90°,∠A=线段AB与x轴正半轴夹角,根据点A(-1,-2),点B(3,4),求得AC=4,BC=6,由勾股定理得到AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{13}$,然后根据三角函数的定义即可得到结论.
解答 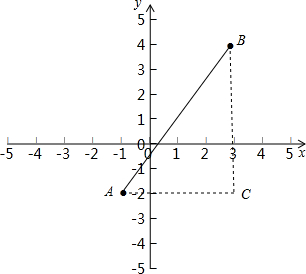 解:如图,过A作AC∥x轴,过B作BC∥y轴,
解:如图,过A作AC∥x轴,过B作BC∥y轴,
则∠C=90°,∠A=线段AB与x轴正半轴夹角,
∵点A(-1,-2),点B(3,4),
∴AC=4,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{13}$,
∴sin∠A=$\frac{BC}{AB}$=$\frac{6}{2\sqrt{13}}$=$\frac{3\sqrt{13}}{13}$.
故选C.
点评 本题考查了解直角三角形,坐标与图形的性质,正确的作出图形是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图,AC平分∠BAF,∠B=80°,∠C=50°,求证:EF∥BC.
如图,AC平分∠BAF,∠B=80°,∠C=50°,求证:EF∥BC.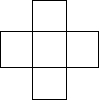 如图是一个由5个相同的正方形组成的十字形的纸片,把这一纸片沿一条直线裁成两部分,然后把其中的一部分再沿着另一条直线截成两部分,使所得的三部分纸片通过适当的拼接能组成两个并列的全等的正方形.请在图中画出分割线及拼接后的图形.
如图是一个由5个相同的正方形组成的十字形的纸片,把这一纸片沿一条直线裁成两部分,然后把其中的一部分再沿着另一条直线截成两部分,使所得的三部分纸片通过适当的拼接能组成两个并列的全等的正方形.请在图中画出分割线及拼接后的图形.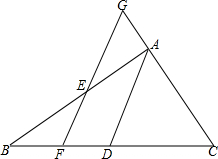 如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F
如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F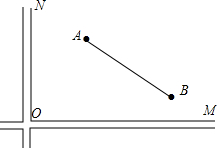 如图,在两条相互垂直的高速公路0M、0N旁有两个相距50km的风景区A和B,A、B到0M的距离分别为40kn和10km,A到0N的距离为30km,现打算在0M旁和0N旁各修建一服务区C、D,使A、B、C、D构成的四边形的周长最小,求出这个最小值(高速公路的宽忽略不计).
如图,在两条相互垂直的高速公路0M、0N旁有两个相距50km的风景区A和B,A、B到0M的距离分别为40kn和10km,A到0N的距离为30km,现打算在0M旁和0N旁各修建一服务区C、D,使A、B、C、D构成的四边形的周长最小,求出这个最小值(高速公路的宽忽略不计).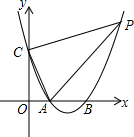 如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.
如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.