题目内容
1.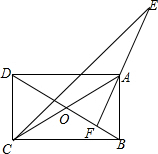 如图,已知矩形ABCD中,AC,BD交于点O,AF⊥BD垂足为F,∠BCD的平分线交FA的延长线于点E,求证:AC=AE.
如图,已知矩形ABCD中,AC,BD交于点O,AF⊥BD垂足为F,∠BCD的平分线交FA的延长线于点E,求证:AC=AE.
分析 首先设BD交CE于点M,由矩形ABCD中,EC平分∠BCD,可得∠ECA=45°-∠OCB,∠EMF=45°+∠OCB,又由AF⊥BD,易证得∠ECA=∠E,继而证得结论.
解答 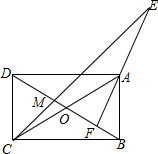 证明:设BD交CE于M,
证明:设BD交CE于M,
∵四边形ABCD是矩形,
∴∠BCD=90°,AC=BD,OA=OC,OB=OD,
∴OC=OB,
∴∠OCB=∠OBC,
∵EC是∠BCD的平分线,
∴∠ECB=45°,
∴∠ECA=∠ECB-∠OCB=45°-∠OCB,∠EMF=∠OBC+∠ECB=45°+∠OCB,
∵AF⊥BD,
∴∠E=90°-∠EMF=45°-∠OCB,
∴∠E=∠ECA,
∴AC=AE.
点评 此题考查了矩形的性质以及等腰三角形的判定.注意分别表示出∠E、∠ECA与∠OCB的关系是解此题的关键.

练习册系列答案
相关题目
10.某同学买了x枚1元的邮票与y枚2元的邮票,共12枚,花了20元钱,列出关于x、y的二元一次方程组为( )
| A. | $\left\{\begin{array}{l}x+y=12\\ 2x+y=20\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=12\\ x+2y=20\end{array}\right.$ | C. | $\left\{\begin{array}{l}x+y=20\\ x+2y=12\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=20\\ 2x+y=12\end{array}\right.$ |
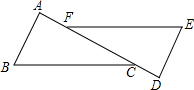 如图,已知A,F,C在一条直线上,且AF=DC,AB∥DE,EF∥CB,求证:BC=EF.
如图,已知A,F,C在一条直线上,且AF=DC,AB∥DE,EF∥CB,求证:BC=EF.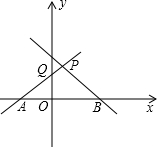 如图,直线y=x+n(n>0)交x轴于A,交y轴于Q,直线y=-2x+m(m>n)交x轴于B,交AQ于P.
如图,直线y=x+n(n>0)交x轴于A,交y轴于Q,直线y=-2x+m(m>n)交x轴于B,交AQ于P.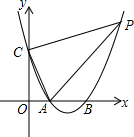 如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.
如图,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,点P在第一象限的抛物线上,且在对称轴右边,S△PAC=10,求点P的坐标.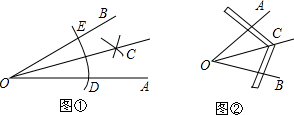
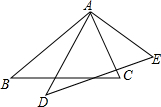 如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度.
如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度.