题目内容
20. 如图,在△ABC中,∠C=90°,分别以A、B为圆心,以相等长度(大于$\frac{1}{2}$AB的长度)为半径画弧,得到两个交点M、N,作直线MN分别交AC、AB于E、D两点,连接EB,若∠EBC=28°,求∠A的度数.
如图,在△ABC中,∠C=90°,分别以A、B为圆心,以相等长度(大于$\frac{1}{2}$AB的长度)为半径画弧,得到两个交点M、N,作直线MN分别交AC、AB于E、D两点,连接EB,若∠EBC=28°,求∠A的度数.
分析 根据直角三角形两锐角互余可得∠A+∠CBA=90°,由作图可得MN是AB的垂直平分线,由线段垂直平分线的性质可得AE=EB,再根据等边对等角可得∠A=∠EBA,然后再由∠EBC=28°可计算出∠A的度数.
解答 解:∵∠C=90°,
∴∠A+∠CBA=90°,
由作图可得MN是AB的垂直平分线,
∴AE=EB,
∴∠A=∠EBA,
∵∠EBC=28°,
∴∠A=$\frac{1}{2}$(90°-28°)=31°.
点评 此题主要考查了线段垂直平分线的性质,以及三角形内角和定理,关键是掌握线段垂直平分线的作法.

练习册系列答案
相关题目
10.若一元二次方程x2+2x+a=0有实数根,则a的取值范围是( )
| A. | a≤1 | B. | a≤4 | C. | a<1 | D. | a≥1 |
11.计算3a2÷$\frac{1}{3}$a4=( )
| A. | 9a6 | B. | a6 | C. | $\frac{9}{{a}^{-2}}$ | D. | $\frac{9}{{a}^{2}}$ |
9.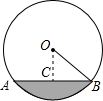 一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )
一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )
 一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )
一条排水管的截面如下左图所示,已知排水管的半径OB=10,水面宽AB=16,则排水管内水的最大深度是( )| A. | 4 | B. | 5 | C. | 6$\sqrt{3}$ | D. | 6 |
 如图,在四边形ABCD中,∠DAB的平分线与∠ABC的平分线相交于E.∠C+∠D=220°,求∠E的度数.
如图,在四边形ABCD中,∠DAB的平分线与∠ABC的平分线相交于E.∠C+∠D=220°,求∠E的度数. 如图,直线AB、CD相交于O,MO⊥AB于O,∠BOC:∠BON=4:1,OM平分∠NOC.求∠MON、∠BOD的度数.
如图,直线AB、CD相交于O,MO⊥AB于O,∠BOC:∠BON=4:1,OM平分∠NOC.求∠MON、∠BOD的度数. 如图,平行四边形ABCD中,E、F分别为AB、AD上的点,且BE=2AE,AF=3DF,连结EF、AC,交于点G,则$\frac{AG}{CG}$的值为$\frac{3}{10}$.
如图,平行四边形ABCD中,E、F分别为AB、AD上的点,且BE=2AE,AF=3DF,连结EF、AC,交于点G,则$\frac{AG}{CG}$的值为$\frac{3}{10}$.