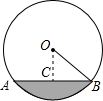一条排水管的截面如下左图所示.已知排水管的半径OB=10.水面宽AB=16.则排水管内水的最大深度是( )A．4B．5C．6$\sqrt{3}$D．6 题目和参考答案——青夏教育精英家教网—

题目内容

9．

一条排水管的截面如下左图所示，已知排水管的半径OB=10，水面宽AB=16，则排水管内水的最大深度是（　　）

A．

B．

C．

6$\sqrt{3}$

D．

分析过O作OD⊥AB交AB于C，交圆于点D，根据垂径定理求出BC的长，再根据勾股定理求出OC的长，由CD=OD-OC即可得出结论．

解答解：过O作OD⊥AB交AB于C，交圆于点D，如图所示：
∴OD=OB=10，
∵AB=16，
∴由垂径定理得：BC=$\frac{1}{2}$AB=8，
∴OC=$\sqrt{O{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∴CD=OD-OC=10-6=4．
故选A．

点评本题考查了垂径定理的应用、勾股定理等知识；熟练掌握垂径定理与勾股定理是解决问题的关键．

练习册系列答案

精英口算卡系列答案

小学生每日10分钟系列答案

天利38套高中名校期中期末联考测试卷系列答案

20．

如图，在△ABC中，∠C=90°，分别以A、B为圆心，以相等长度（大于$\frac{1}{2}$AB的长度）为半径画弧，得到两个交点M、N，作直线MN分别交AC、AB于E、D两点，连接EB，若∠EBC=28°，求∠A的度数．

17．

已知直线y=-$\frac{4}{3}$x+4与x轴和y轴分别交与A、B两点，另一直线过点A和点C（7，3）．
（1）求直线AC对应的函数关系式；
（2）求证：AB⊥AC；
（3）若点P是直线AC上的一个动点，点Q是x轴上的一个动点，且以P、Q、A为顶点的三角形与△AOB全等，求点Q的坐标．

14．多项式A与多项式B的和是3x+x²，多项式B与多项式C的和是-x+3x²，那么多项式A减去多项式C的差是4x-2x²．

1．某村种的水稻前年平均每公顷产7 200kg，今年平均每公顷产8 450kg．设这两年该村水稻每公顷产量的年平均增长率为x，根据题意，所列方程为7200（1+x）²=8450．

18．我们知道平方运算和开方运算是互逆运算，如：a²±2ab+b²=（a±b）²，那么$\sqrt{{a^2}±2ab+{b^2}}=|a±b|$，那么如何将双重二次根式$\sqrt{a±2\sqrt{b}}$$（a＞0，b＞0，a±2\sqrt{b}＞0）$
化简呢？如能找到两个数m，n（m＞0，n＞0），使得${（\sqrt{m}）^2}+{（\sqrt{n}）^2}=a$即m+n=a，且使$\sqrt{m}•\sqrt{n}=\sqrt{b}$即m•n=b，那么$a±2\sqrt{b}={（\sqrt{m}）^2}+{（\sqrt{n}）^2}±2\sqrt{m}•\sqrt{n}={（\sqrt{m}±\sqrt{n}）^2}$∴$\sqrt{a±2\sqrt{b}}=|\sqrt{m}±\sqrt{n}|$，双重二次根式得以化简；
例如化简：$\sqrt{3+2\sqrt{2}}$；∵3=1+2且2=1×2，∴$3+2\sqrt{2}={（\sqrt{1}）^2}+{（\sqrt{2}）^2}+2\sqrt{1}×\sqrt{2}$∴$\sqrt{3+2\sqrt{2}}=1+\sqrt{2}$
由此对于任意一个二次根式只要可以将其化成$\sqrt{a±2\sqrt{b}}$的形式，且能找到m，n（m＞0，n＞0）使得m+n=a，且m•n=b，那么这个双重二次根式一定可以化简为一个二次根式．请同学们通过阅读上述材料，完成下列问题：
（1）填空：$\sqrt{5-2\sqrt{6}}$=$\sqrt{3}$-$\sqrt{2}$； $\sqrt{12+2\sqrt{35}}$=$\sqrt{7}$+$\sqrt{5}$；
（2）化简：①$\sqrt{9+6\sqrt{2}}$②$\sqrt{16-4\sqrt{15}}$
（3）计算：$\sqrt{3-\sqrt{5}}+\sqrt{2+\sqrt{3}}$．

7．

如图，在矩形ABCD中，两条对角线AC、BD相交于O，∠ACD=30°，AD=2．
（1）判断△AOD的形状；
（2）求对角线AC的长．

试题分类