题目内容
10.若一元二次方程x2+2x+a=0有实数根,则a的取值范围是( )| A. | a≤1 | B. | a≤4 | C. | a<1 | D. | a≥1 |
分析 首先得出根的判别式△=b2-4ac=4-4a≥0,进一步求得不等式的解集得出答案即可.
解答 解:∵一元二次方程x2+2x+a=0有实数根,
∴△≥0,即△=4-4a≥0,
∴a≤1.
故选:A.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
20.下列四个实数中是无理数是( )
| A. | 0 | B. | π | C. | $\frac{22}{7}$ | D. | $\sqrt{16}$ |
5.一元二次方程x2-x-2=0的解是( )
| A. | x1=-1,x2=-2 | B. | x1=1,x2=-2 | C. | x1=1,x2=2 | D. | x1=-1,x2=2 |
 如图,已知∠α,用直尺和三角尺画图:
如图,已知∠α,用直尺和三角尺画图: 如图,扇形OMN与正方形ABCD,半径OM与边AB重合,弧MN的长等于AB的长,已知AB=2,扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止,则点O经过的路径长2+4π.
如图,扇形OMN与正方形ABCD,半径OM与边AB重合,弧MN的长等于AB的长,已知AB=2,扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止,则点O经过的路径长2+4π.
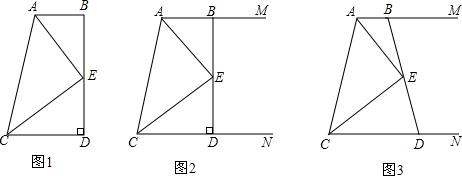
 如图,在△ABC中,∠C=90°,分别以A、B为圆心,以相等长度(大于$\frac{1}{2}$AB的长度)为半径画弧,得到两个交点M、N,作直线MN分别交AC、AB于E、D两点,连接EB,若∠EBC=28°,求∠A的度数.
如图,在△ABC中,∠C=90°,分别以A、B为圆心,以相等长度(大于$\frac{1}{2}$AB的长度)为半径画弧,得到两个交点M、N,作直线MN分别交AC、AB于E、D两点,连接EB,若∠EBC=28°,求∠A的度数.