题目内容
19. 如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC外接圆的半径为$\sqrt{3}$cm.
如图,在△ABC中,BC=3cm,∠BAC=60°,那么△ABC外接圆的半径为$\sqrt{3}$cm.
分析 连接BO、CO,作OD⊥BC,垂足为D.求出∠OBC的度数,再根据三角函数解答.
解答  解:如图,连接BO、CO,作OD⊥BC,垂足为D.
解:如图,连接BO、CO,作OD⊥BC,垂足为D.
∵∠BAC=60°,
∴∠BOC=2×60°=120°,
∵OD⊥BC,
∴BD=CD=3×$\frac{1}{2}$=$\frac{3}{2}$,
∴BO=$\frac{\frac{3}{2}}{cos30°}$=$\frac{3}{2}$×$\frac{2}{\sqrt{3}}$=$\sqrt{3}$cm,
故答案为$\sqrt{3}$.
点评 本题考查了圆周角定理、垂径定理、解直角三角形,综合性较强.

练习册系列答案
相关题目
10.下面图形中既是轴对称图形,又是中心对称图形的是( )
| A. | 平行四边形 | B. | 等腰梯形 | C. | 正三角形 | D. | 菱形 |
14.下列运算正确的是( )
| A. | 2(a+b)=2a+b | B. | (a-b)2=a2-b2 | C. | a5÷a3=a2 | D. | a2b+ab2=a3b3 |
4.下列计算正确的是( )
| A. | 3m2•m=3m3 | B. | (2m)3=6m3 | C. | (a+b)2=a2+b2 | D. | 3mn-3n=m |
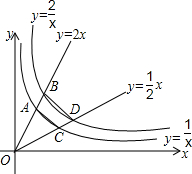 如图,直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,则四边形ABCD的面积为$\frac{3}{4}$.
如图,直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,则四边形ABCD的面积为$\frac{3}{4}$. 超速行驶是引发交通事故的主要原因之一,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,距离大路(BC)为30米,一辆小轿车由西向东匀速行驶,测得此车从B处到C处所用的时间为5秒,∠BAC=60°.
超速行驶是引发交通事故的主要原因之一,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,距离大路(BC)为30米,一辆小轿车由西向东匀速行驶,测得此车从B处到C处所用的时间为5秒,∠BAC=60°.
 如图,在△ABC中,BC=2AC,∠C=2∠B,求证:∠A=90°.
如图,在△ABC中,BC=2AC,∠C=2∠B,求证:∠A=90°.