题目内容
14.已知:$\sqrt{\frac{9-x}{x-6}}$=$\frac{\sqrt{9-x}}{\sqrt{x-6}}$,且x是偶数,求:代数式(x+2)$\sqrt{\frac{x-2}{x+2}}$的值.分析 直接利用二次根式的定义得出x的取值范围,进而得出x的值,进而化简得出答案.
解答 解:由$\sqrt{\frac{9-x}{x-6}}$=$\frac{\sqrt{9-x}}{\sqrt{x-6}}$,可得:
$\left\{\begin{array}{l}{9-x≥0}\\{x-6>0}\end{array}\right.$
所以,解得:6<x≤9,
又因为x是偶数,所以x=8,
所以(x+2)$\sqrt{\frac{x-2}{x+2}}$=(8+2)$\sqrt{\frac{8-2}{8+2}}$=10$\sqrt{\frac{6}{10}}$=2$\sqrt{15}$.
点评 此题主要考查了二次根式的乘除法,正确得出x的值是解题关键.

练习册系列答案
相关题目
2.与$\sqrt{2}$-$\sqrt{3}$互为倒数的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$ | B. | $\sqrt{2}$-$\sqrt{3}$ | C. | $\sqrt{3}$-$\sqrt{2}$ | D. | -$\sqrt{2}$-$\sqrt{3}$ |
19.若不等式ax<5的解集是x>-1,则a的值为( )
| A. | -15 | B. | -5 | C. | -6 | D. | -9 |
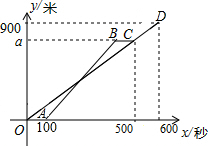 小明、小亮从宝安中心图书馆出发,沿相同的线路跑向宝安体育场,小明先跑一点路程后,小亮开始出发,当小亮超过小明150米时,小亮停在此地等候小明,两人相遇后,一起以小明原来的速度跑向宝安体育场,如图,反映了两人所跑路程y(米)与所用时间x(秒)之间的关系,请根据题意解答下列问题:
小明、小亮从宝安中心图书馆出发,沿相同的线路跑向宝安体育场,小明先跑一点路程后,小亮开始出发,当小亮超过小明150米时,小亮停在此地等候小明,两人相遇后,一起以小明原来的速度跑向宝安体育场,如图,反映了两人所跑路程y(米)与所用时间x(秒)之间的关系,请根据题意解答下列问题: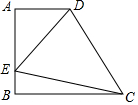 如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.