题目内容
18.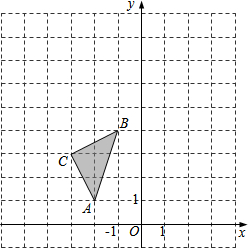 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,3).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,3).(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1点的坐标及sin∠B1A1C1的值;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出 将△ABC放大后的△A2B2C2,并写出A2点的坐标;
(3)若点D(a,b)在线段AB上,直接写出经过(2)的变化后点D的对应点D2的坐标.
分析 (1)利用关于y轴对称点的性质得出对应点坐标进而求出即可;
(2)利用位似图形的性质得出对应点位置即可得出答案;
(3)利用位似比得出对应点坐标的变化规律进而得出答案.
解答 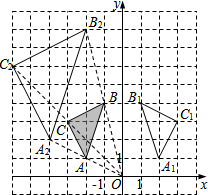 解:(1)如图,△A1B1C1,即为所求,
解:(1)如图,△A1B1C1,即为所求,
A1(2,1),
∵${{B}_{1}A}_{1}^{2}$=B1C${\;}_{1}^{2}$+A1C${\;}_{1}^{2}$,A1C1=B1C1,
∴△A1B1C1是等腰直角三角形,
∴sin∠B1A1C1=sin45°=$\frac{{\sqrt{2}}}{2}$;
(2)如图,△A2B2C2,即为所求,
A2(-4,2);
(3)∵点D(a,b)在线段AB上,位似比为1:2,
∴D2(2a,2b).
点评 此题主要考查了位似图形的性质以及位似变换和轴对称变换,得出对应点位置是解题关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,∠1的同位角是∠B,∠B的内错角是∠3,∠4与∠B是同旁内角.
如图,∠1的同位角是∠B,∠B的内错角是∠3,∠4与∠B是同旁内角.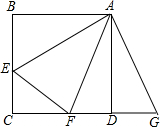 正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG.求证:EF=BE+DF.
正方形ABCD中,E,F分别是边BC,CD上的点,且∠EAF=45°,将△ABE绕点A逆时针旋转90°,得到△ADG.求证:EF=BE+DF.
 如图所示,三角形AOB绕着点O旋转至三角形A1OB1,若∠AOA1=60°,∠BOA1=28°,则∠A1OB1=32°.
如图所示,三角形AOB绕着点O旋转至三角形A1OB1,若∠AOA1=60°,∠BOA1=28°,则∠A1OB1=32°.