题目内容
20.在平面直角坐标系中,点B、A分别在x轴和y轴上,连接AB,已知∠ABO=60°,BC平分∠ABO交y轴于点C,且BC=8.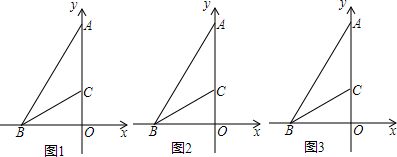
(1)求点A的坐标;
(2)点P从点B出发,沿射线BC方向以每秒2个长度单位的速度运动,过点P作PQ⊥y轴于Q,设点P的运动时间为t秒,试用t表示线段CQ的长;
(3)点D是点B关于y轴的对称点,在(2)的条件下,连接OP、DQ、CD,当$S{\;}_{△BOP}=\frac{9}{5}{S_{△DCQ}}$时,求t的值.
分析 (1)首先在直角△BOC中,利用三角函数求得OC的长,然后证明BC=AC,则求得OA的长,得到A的坐标;
(2)分成P在线段BC上和在BC的延长线上两种情况进行讨论,利用三角函数求解;
(3)同(2)分成两种情况讨论,根据三角形面积公式利用t表示出△BPO和△DCQ的面积,然后解方程即可求解.
解答  解:(1)∵∠ABO=60°,BC是角平分线,
解:(1)∵∠ABO=60°,BC是角平分线,
∴∠ABC=∠CBO=30°,
在直角△BOC中,OC=BC•sin∠CBO=$\frac{1}{2}$BC=4,即C的坐标是(0,4).
又∵直角△ABO中,∠BAO=90°-∠ABO=90°-60°=30°,
∴∠BAO=∠ABC=30°,
∴AC=BC=8,
∴OA=8+4=12,
∴A的坐标是(0,12);
(2)当0≤t≤4时,如图1,P在BC上,BP=2t,则PC=8-2t,
在直角△PCQ中,∠CPQ=∠CBO=30°,
则CQ=$\frac{1}{2}$PC=$\frac{1}{2}$(8-2t)=4-t;
当t>4时,P在BC的延长线上,如图2.
BP=2t,则CP=2t-8,
在直角△PCQ中,∠CPQ=30°,CQ=$\frac{1}{2}$PC=$\frac{1}{2}$(2t-8)=4-4;
(3)在直角△BOC中,OB=BC•cos∠CBO=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,则B的坐标是(-4$\sqrt{3}$,0),则D的坐标是(4$\sqrt{3}$,0).
当0≤t≤4时,如图1,P在线段BC上,作PF⊥OB于点F.则PF=$\frac{1}{2}$BP=t,则S△BOP=$\frac{1}{2}$×4$\sqrt{3}$t=2$\sqrt{3}$t,
CQ=4-t,则S△DCQ=$\frac{1}{2}$(4-t)×4$\sqrt{3}$=-2$\sqrt{3}$t+8$\sqrt{3}$,
当$S{\;}_{△BOP}=\frac{9}{5}{S_{△DCQ}}$时,2$\sqrt{3}$t=$\frac{9}{5}$(-2$\sqrt{3}$t+8$\sqrt{3}$),解得:t=$\frac{18}{7}$;
当t>4时,P在BC的延长线上,如图2.作PF⊥OB于点F.则PF=$\frac{1}{2}$BP=t,则S△BOP=$\frac{1}{2}$×4$\sqrt{3}$t=2$\sqrt{3}$t,
CQ=4-t,则S△DCQ=$\frac{1}{2}$(t-4)×4$\sqrt{3}$=2$\sqrt{3}$t-8$\sqrt{3}$,
当$S{\;}_{△BOP}=\frac{9}{5}{S_{△DCQ}}$时,2$\sqrt{3}$t=$\frac{9}{5}$(2$\sqrt{3}$t-8$\sqrt{3}$),解得:t=9.
总之,t=$\frac{18}{7}$或9.
点评 本题考查了三角函数,以及点的运动变化,注意分成两种情况,利用t表示出△BPO和△DCQ的面积是本题的关键.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | -5是25的平方根 | B. | 25的平方根是-5 | ||
| C. | $\sqrt{16}$是$\root{3}{-27}$的算术平方根 | D. | $\sqrt{3}$是$\sqrt{{{(-3)}^2}}$的算术平方根 |
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
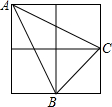 如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中AB边上的高是$\frac{3\sqrt{5}}{5}$.
如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中AB边上的高是$\frac{3\sqrt{5}}{5}$.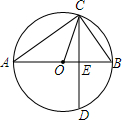 如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.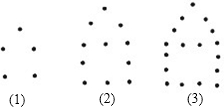 如图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,摆第四个要23枚棋子,摆第30个“小屋子”要179枚棋子.
如图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,摆第四个要23枚棋子,摆第30个“小屋子”要179枚棋子.