题目内容
15．
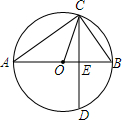如图，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E．连接AC、OC、BC．（1）求证：∠ACO=∠BCD．
（2）若BE=3，CD=8，求BC的长．
分析 （1）根据圆周角定理得到∠ACB=90°，根据直角三角形的性质和等腰三角形的性质得到答案；
（2）根据垂径定理得到CE的长，根据勾股定理计算即可．
解答 解：（1）∵AB为⊙O的直径，
∴∠ACB=90°，
∴∠A+∠B=90°，
∵AB⊥CD，
∴∠BCD+∠B=90°，
∴∠A=∠BCD，
∵OA=OC，
∴∠A=∠ACO，
∴∠ACO=∠BCD；
（2）∵AB⊥CD，
∴CE=$\frac{1}{2}$CD=4，
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=5．
点评 本题考查的是圆周角定理、垂径定理、勾股定理，灵活运用相关定理是解题的关键．
练习册系列答案
相关题目
6．已知m、n均为非零有理数，下列结论正确的是（ ）
| A． | 若m≠n，则|m|≠|n| | B． | 若|m|=|n|，则m=n | C． | 若m＞n＞0，则$\frac{1}{m}$＞$\frac{1}{n}$ | D． | 若m＞n＞0，则m2＞n2 |
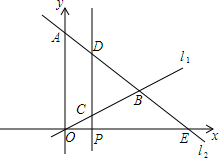如图，在平面直角坐标系中，点A的坐标为（0，24），经过原点的直线l1与经过点A的直线l2相交于点B，点B的坐标为（18，6）．在x轴上有一点P（a，0），过点P作x轴的垂线分别交直线l1、l2于点C、D，直线l2与x轴交于点E．
10．
如图，在平面直角坐标系中，点A，B，C的坐标为（1，4），（5，4），（1，-2），则△ABC外接圆的圆心坐标是（ ）
如图，在平面直角坐标系中，点A，B，C的坐标为（1，4），（5，4），（1，-2），则△ABC外接圆的圆心坐标是（ ）| A． | （2，3） | B． | （3，2） | C． | （1，3） | D． | （3，1） |
