题目内容
18.(1)计算:$\sqrt{12}$+|2-$\sqrt{3}$|+($\sqrt{3}$)2(2)解方程:$\frac{3}{x-1}$=$\frac{6}{{x}^{2}-1}$.
分析 (1)先把二次根式化为最简二次根式,然后去绝对值后合并即可;
(2)先把方程化为整式方程,解整式方程得到x=1,然后进行检验确定原方程的解.
解答 (1)解:原式=$2\sqrt{3}+2-\sqrt{3}+3$
=$\sqrt{3}+5$;
(2)解:去分母得3(x+1)=6,解得x=1,
检验:把x=1代入x2-1=0,则x=1为原方程的增根,
所以原方程无解.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解分式方程.

练习册系列答案
相关题目
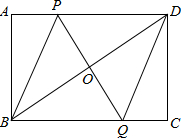 如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.
如图,在矩形ABCD中,P是AD上一动点,O为BD的中点,连接PO并延长,交BC于点Q.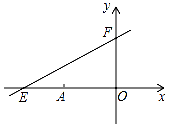 如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.
如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0),P(x,y)是直线y=kx+6上的一个动点.