题目内容
6.计算:(1)9×(-$\frac{1}{3}$)2+$\sqrt{4}$-|-3|
(2)$\left\{\begin{array}{l}{3x-y=7}\\{x+3y=-1}\end{array}\right.$
(3)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$,并将不等式组的解集在所给数轴上表示出来.
分析 (1)分别进行平方、开平方、绝对值的化简等运算,然后计算乘法,最后合并;
(2)方程组利用加减消元法求出解即可;
(3)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集.
解答 解:(1)9×(-$\frac{1}{3}$)2+$\sqrt{4}$-|-3|
=9×$\frac{1}{9}$+2-3
=1+2-3
=0
(2)$\left\{\begin{array}{l}{3x-y=7①}\\{x+3y=-1②}\end{array}\right.$
①×3+②得:10x=20,即x=2,
把x=2代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$
解不等式①得:x≤1,
解不等式②得:x>-2,
原不等式红的解为:-2<x≤1.
不等式组的解集在数轴上表示: .
.
点评 此题考查了实数的运算,解二元一次方程组,解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.投掷一枚质地均匀的骰子一次,正面是偶数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
1.下面计算正确的是( )
| A. | 4a-3a=1 | B. | a2+a3=a5 | C. | x6÷x3=x2 | D. | (-2a3)2=4a6 |
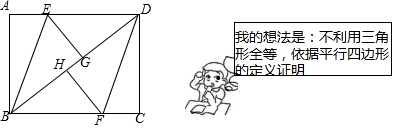
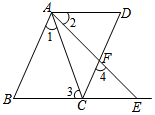 完成下面推理步骤,并在每步后面的括号内填写出推理根据:
完成下面推理步骤,并在每步后面的括号内填写出推理根据: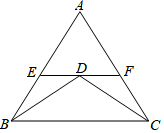 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.