题目内容
12.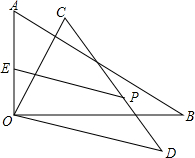 如图在△ABO中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为x(0°<x<180°)得到△COD.设AO中点为E,CD中点为P,AO=6,连接EP,当旋转角x=120°时,EP长度最大,最大值为9.
如图在△ABO中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为x(0°<x<180°)得到△COD.设AO中点为E,CD中点为P,AO=6,连接EP,当旋转角x=120°时,EP长度最大,最大值为9.
分析 根据含30度的直角三角形三边的关系得到AB=2OA=12,再根据旋转的性质CD=AB=12,连结OP,根据直角三角形斜边上的中线性质得OP=$\frac{1}{2}$CD=6,如图1,根据三角形三边的关系得PE<OE+OP,点P、O、E共线时,PE=OE+OP,如图2,点Q为AB的中点,此时PE最大,易得PE的最大值为9,然后求出∠AOP的度数即可得到旋转角的度数.
解答 解:∵∠AOB=90°,∠ABO=30°,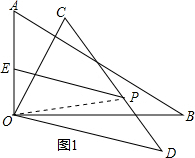
∴AB=2OA=12,
∵△AOB绕顶点O顺时针旋转,旋转角为x(0°<x<180°)得到△COD,
∴CD=AB=12,
连结OP,
∵CD中点为P,
∴OP=$\frac{1}{2}$CD=6,
如图1,PE<OE+OP,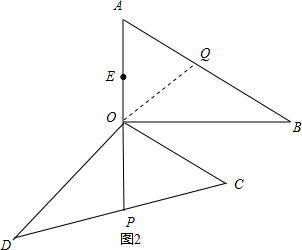 点P、O、E共线时,如图2,Q为AB的中点,
点P、O、E共线时,如图2,Q为AB的中点,
∵PE=OE+OP,
∴PE的最大值为3+6=9.
∵QA=QO,
∴∠AOQ=∠A=60°,
∴∠POQ=120°
∴旋转角x=120°.
故答案为120°,9.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了直角三角形斜边上的中线性质.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
4.下列运算正确的是( )
| A. | a0=1 | B. | 3a•4a=12a | C. | a12÷a3=a4 | D. | (a3)4=a12 |
2. 将三角板与直尺按如图所示的方式叠放在一起,在图中标记的角中,与∠6互余的角共有( )
将三角板与直尺按如图所示的方式叠放在一起,在图中标记的角中,与∠6互余的角共有( )
 将三角板与直尺按如图所示的方式叠放在一起,在图中标记的角中,与∠6互余的角共有( )
将三角板与直尺按如图所示的方式叠放在一起,在图中标记的角中,与∠6互余的角共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
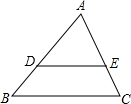 如图,△ABC中,DE∥BC,且AD:DB=2:1,那么DE:BC=2:3.
如图,△ABC中,DE∥BC,且AD:DB=2:1,那么DE:BC=2:3.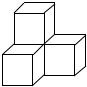 如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( )
如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( )