题目内容
7.直角三角形中,两直角边的比是2:3,且斜边长为$\sqrt{39}$,则其面积为9.分析 先根据比值设出直角三角形的两直角边,用勾股定理求出未知数x,即两条直角边,用面积公式计算即可.
解答 解:设直角三角形的两直角边分别为3x,2x(x>0),
根据勾股定理得,(3x)2+(2x)2=39,
∴x=$\sqrt{3}$或x=-$\sqrt{3}$(舍),
∴3x=2$\sqrt{3}$,3x=3$\sqrt{3}$
∴直角三角形的两直角边分别为2$\sqrt{3}$,3$\sqrt{3}$,
∴直角三角形的面积为$\frac{1}{2}$×2$\sqrt{3}$×3$\sqrt{3}$=9,
故答案为9.
点评 此题是勾股定理的应用,主要考查了勾股定理,三角形的面积计算方法,解本题的关键是用勾股定理求出直角边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列选项中所表示的数,哪一个与252的最大公因数为42( )
| A. | 2×3×52×72 | B. | 2×32×5×72 | C. | 22×3×52×7 | D. | 22×32×5×7 |
7.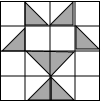 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
 如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.
如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.